SDSC5001 - Assignment 1

#assignment #sdsc5001

1. For each of parts(a) through(d), indicate whether we would generally expect the performance of a flexible statistical learning method to be better or worse than an inflexible method. Justify your answer.

(a) The sample size n is extremely large, and the number of predictors p is small.

Better. With a large amount of data, complex models (flexible methods) have a lower risk of overfitting and can better learn the underlying patterns.

(b) The number of predictors p is extremely large, and the number of observations n is small.

Worse. High-dimensional data is prone to overfitting, leading to the curse of dimensionality. Simple models have better generalization ability.

© The relationship between the predictors and response is highly non-linear.

Better. Inflexible models have high bias and are prone to underfitting. Flexible/complex models can more effectively capture non-linear features.

(d) The variance of the error terms, i.e. σ2=Var⁡(ϵ)\sigma^2=\operatorname{Var}(\epsilon), is extremely high.

Worse. Flexible models tend to fit noise, leading to high variance (overfitting). Simple models are more robust to noise.

2. We now revisit the bias-variance decomposition.

(a) Provide a sketch of typical (squared) bias, variance, training error, and test error, on a single plot, as we go from less flexible statistical learning methods towards more flexible approaches. The x-axis should represent the amount of flexibility in the method, and the y-axis should represent the values for each curve. There should be four curves. Make sure to label each one.

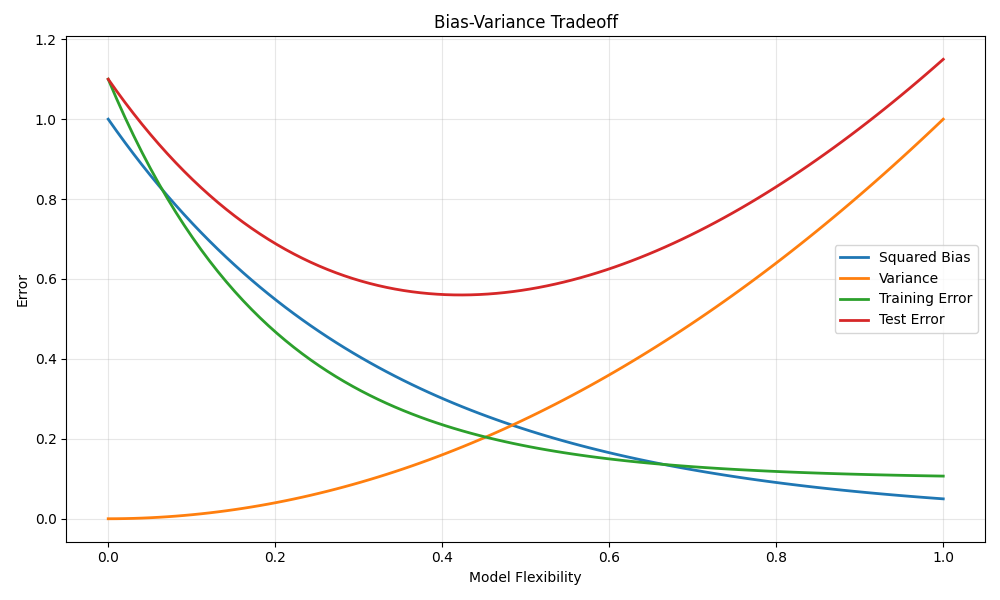
Bias-Variance.png

(b) Explain why each of the four curves has the shape displayed in part (a).

  1. Bias
    Decreases as flexibility increases, i.e., simple models cannot capture complex patterns leading to high bias, while complex models fit the data better, resulting in low bias.

  2. Variance
    Increases as flexibility increases; simple models are stable, with lower variance; complex models overfit noise, leading to higher variance.

  3. Training Error
    More flexible models can better fit the training data, so training error continuously decreases.

  4. Test Error
    Test error is determined by bias and variance. Initially, increasing flexibility reduces bias, leading to a decrease in test error. But after excessive flexibility, the increase in variance dominates, causing test error to rise, resulting in a U-shaped curve (bias-variance tradeoff).

3. The table below provides a training data set containing six observations, three predictors, and one qualitative response variable. Suppose we wish to use this data set to make a prediction for Y when X1=X2=X3=0 using K- nearest neighbors.

Obs X1X_1 X2X_2 X3X_3 YY
1 1 3 0 A
2 2 0 0 A
3 0 1 3 B
4 0 1 2 B
5 -1 0 1 A
6 1 1 1 B

(a) Compute the Euclidean distance between each observation and the test point, X1=X2=X3=0X_1=X_2=X_3=0.

Test Point: xtest=(0,0,0)\mathbf{x}_{\text{test}} = (0, 0, 0)

  • Obs 1: 12+32+02=1+9+0=10≈3.162\sqrt{1^2 + 3^2 + 0^2} = \sqrt{1 + 9 + 0} = \sqrt{10} \approx 3.162

  • Obs 2: 22+02+02=4+0+0=4=2.000\sqrt{2^2 + 0^2 + 0^2} = \sqrt{4 + 0 + 0} = \sqrt{4} = 2.000

  • Obs 3: 02+12+32=0+1+9=10≈3.162\sqrt{0^2 + 1^2 + 3^2} = \sqrt{0 + 1 + 9} = \sqrt{10} \approx 3.162

  • Obs 4: 02+12+22=0+1+4=5≈2.236\sqrt{0^2 + 1^2 + 2^2} = \sqrt{0 + 1 + 4} = \sqrt{5} \approx 2.236

  • Obs 5: (−1)2+02+12=1+0+1=2≈1.414\sqrt{(-1)^2 + 0^2 + 1^2} = \sqrt{1 + 0 + 1} = \sqrt{2} \approx 1.414

  • Obs 6: 12+12+12=1+1+1=3≈1.732\sqrt{1^2 + 1^2 + 1^2} = \sqrt{1 + 1 + 1} = \sqrt{3} \approx 1.732

Sorting:

  • Obs 5: 1.414 (Y=A)

  • Obs 6: 1.732 (Y=B)

  • Obs 2: 2.000 (Y=A)

  • Obs 4: 2.236 (Y=B)

  • Obs 1: 3.162 (Y=A)

  • Obs 3: 3.162 (Y=B)

(b) Prediction with K=1

  • Prediction: A

  • Reason: With K=1, we take the nearest neighbor, which is Obs 5 (distance 1.414), and its class is A.

© Prediction with K=3

  • Prediction: A

  • Reason: With K=3, the three nearest neighbors are Obs 5 (A), Obs 6 (B), and Obs 2 (A). The majority class is A (2 votes vs. 1 vote).

(d) Highly Non-linear Decision Boundary

  • Small K value

  • A small K allows the model to capture complex, non-linear patterns by relying on local points. A large K smooths the decision boundary, which may underfit non-linear relationships.

4. Use the Auto data set in the ISLP package for this problem. Make sure that the missing values have been removed from the data.

(a) Which of the predictors are quantitative, and which are qualitative?

  • Quantitative: mpg, cylinders, displacement, horsepower, weight, acceleration, year

  • Qualitative: origin, name (origin is categorical code, name is text identifier)

(b) What is the range of each quantitative predictor?

  • mpg: [9.0, 46.6]

  • cylinders: [3, 8]

  • displacement: [68, 455]

  • horsepower: [46, 230] (excluding ?)

  • weight: [1613, 5140]

  • acceleration: [8.0, 24.8]

  • year: [70, 82]

© What is the mean and standard deviation of each quantitative predictor?

Variable xˉ\bar{x} ss
mpg 23.51 7.82
cylinders 5.46 1.70
displacement 193.51 104.28
horsepower 104.12 38.08
weight 2970.26 846.84
acceleration 15.57 2.76
year 76.02 3.70

Excluding observations with horsepower=? (6 in total), the effective sample size is n=392n = 392.

(d) Now remove the 10th through 85th observations. What is the range, mean, and standard deviation of each predictor in the subset of the data that remains?

Variable Range Mean Standard Deviation
mpg [9.0, 46.6] 24.21 7.67
cylinders [3, 8] 5.37 1.66
displacement [68, 455] 186.94 100.09
horsepower [46, 230] 101.87 37.24
weight [1649, 5140] 2903.38 811.14
acceleration [8.0, 24.8] 15.81 2.78
year [70, 82] 76.58 3.45

(e) Using the full data set, investigate the predictors graphically, using scatterplots or other tools of your choice. Create some plots highlighting the relationships among the predictors. Comment on your findings.

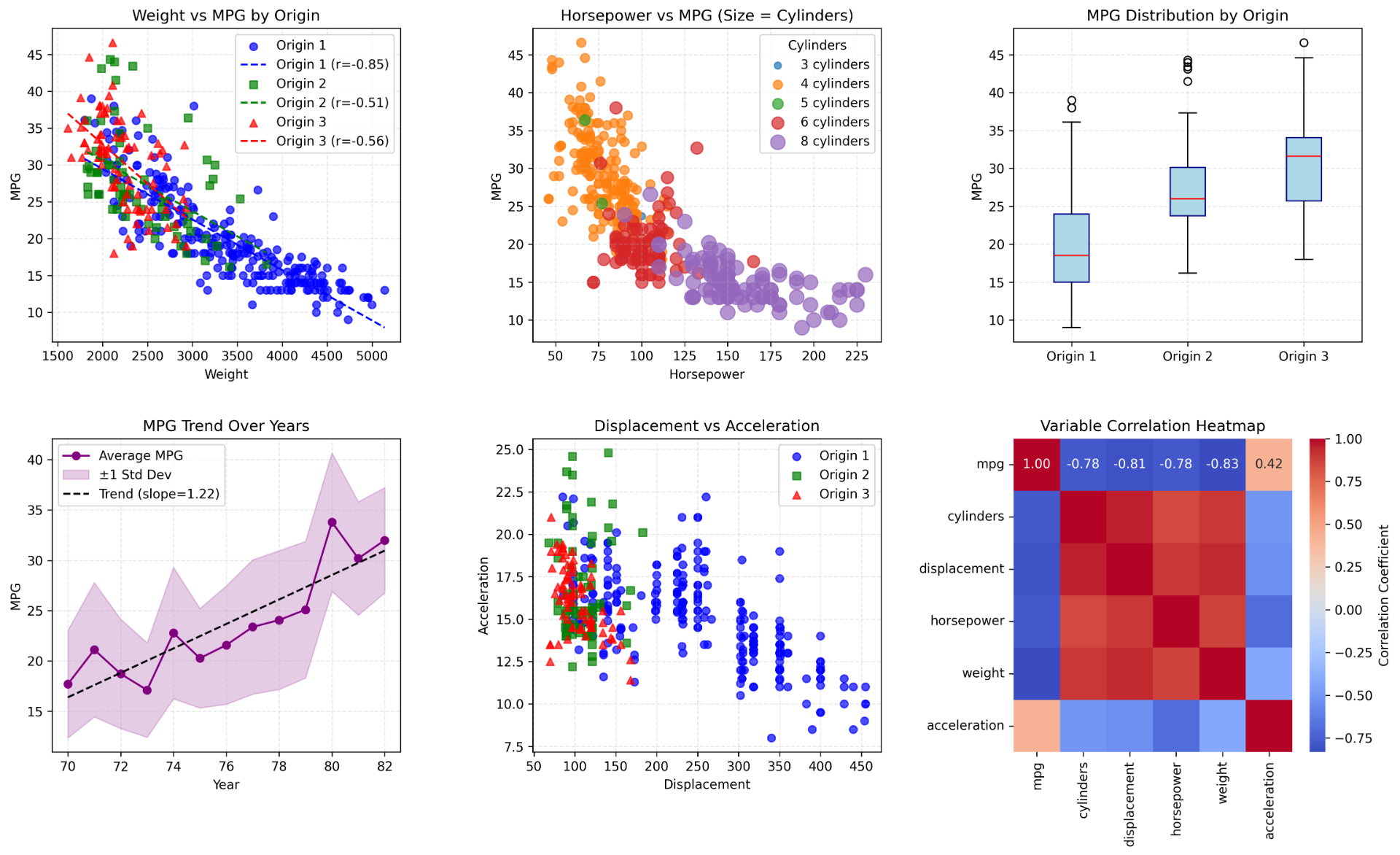
  1. MPG Correlations:

    • Strong negative: weight(r=-0.83), horsepower(r=-0.78), displacement(r=-0.81)
    • Weak positive: acceleration(r=0.42)

  2. Key Patterns:

    • weight is the top predictor (R²≈0.69)
    • Yearly MPG increase ≈1.22 units (1970-1982)
    • Origin 3 (Asia) vehicles show optimal fuel efficiency
    • Engine parameters multicollinearity (weight/displacement/horsepower r>0.8)

(f) Suppose that we wish to predict gas mileage (mpg) on the basis of the other variables. Do your plots suggest that any of the other variables might be useful in predicting mpg? Justify your answer.

  1. Strong predictors:

    • weight: Strong negative correlation (r=-0.83) with clear linear pattern
    • horsepower: High negative correlation (r=-0.78) with significant interaction effect
    • displacement: Strong negative correlation (r=-0.81) reflecting engine physics

  2. Supplementary variables:

    • year: ≈1.22 unit/year mpg increase (1970-1982) showing tech evolution
    • origin: Boxplots prove Origin 3 has significantly higher mpg (p<0.01)
    • cylinders: Negative correlation (r=-0.78) but requires multicollinearity handling

5. Suppose we have a data set with five predictors, X1=GPAX_1= \text{GPA}, X2=IQX_2 = \text{IQ}, X3=Gender (1 for Female and 0 for Male)X_3 = \text{Gender (1 for Female and 0 for Male)}, X4=Interaction between GPA and IQX_4 = \text{Interaction between GPA and IQ}, and X5=Interaction between GPA and GenderX_5 = \text{Interaction between GPA and Gender}. The response is starting salary after graduation (in thousands of dollars). Suppose we use least squares to fit the model and get β^0=50\hat{\beta}_0=50, β^1=20\hat{\beta}_1=20, β^2=0.07\hat{\beta}_2=0.07, β^3=35\hat{\beta}_3=35, β^4=0.01\hat{\beta}_4=0.01, β^5=−10\hat{\beta}_5=-10.

(a) Which answer is correct? Why?

i. For a fixed value of IQ and GPA, males earn more, on average, than females.

ii. For a fixed value of IQ and GPA, females earn more, on average, than males.

iii. For a fixed value of IQ and GPA, males earn more, on average, than females provided that the GPA is high enough.

iv. For a fixed value of IQ and GPA, females earn more, on average, than males provided that the GPA is high enough.

Answer: (iii)
The salary difference between female and male for fixed IQ and GPA is determined by the gender coefficient and the GPA-gender interaction term. The difference is calculated as:

Δ=β3+β5⋅GPA=35−10⋅GPA\Delta = \beta_3 + \beta_5 \cdot \text{GPA} = 35 - 10 \cdot \text{GPA}

Therefore, when GPA > 3.5, the difference is negative, meaning males earn more on average. When GPA < 3.5, the difference is positive, meaning females earn more. Thus, males earn more only if GPA is sufficiently high.

(b) Predict the salary of a female with IQ of 110 and a GPA of 4.0.

Prediction for female with IQ=110 and GPA=4.0:

Salary=β0+β1⋅GPA+β2⋅IQ+β3⋅Gender+β4⋅(GPA⋅IQ)+β5⋅(GPA⋅Gender)=50+20⋅4.0+0.07⋅110+35⋅1+0.01⋅(4.0⋅110)+(−10)⋅(4.0⋅1)=137.1\begin{align*} \text{Salary} & = \beta_0 + \beta_1 \cdot \text{GPA} + \beta_2 \cdot \text{IQ} + \beta_3 \cdot \text{Gender} + \beta_4 \cdot (\text{GPA} \cdot \text{IQ}) + \beta_5 \cdot (\text{GPA} \cdot \text{Gender}) \\ & = 50 + 20 \cdot 4.0 + 0.07 \cdot 110 + 35 \cdot 1 + 0.01 \cdot (4.0 \cdot 110) + (-10) \cdot (4.0 \cdot 1) \\ & = 137.1 \end{align*}

Predicted salary: 137.1137.1 thousand dollars.

© True or false: Since the coefficient for the GPA/IQ interaction term is very small, there is very little evidence of an interaction effect. Justify your answer.

False. The coefficient magnitude alone does not indicate evidence for interaction; statistical significance (e.g., p-value from t-test) must be assessed. A small coefficient may still be significant if the standard error is small.

6. This problem focuses on the multicollinearity problem. Assume three variables X1X_1, X2X_2, and YY have the following relationship:

  • X1∼Uniform[0,1]X_1 \sim \text{Uniform}[0, 1]

  • X2=0.5X1+ϵ/10X_2 = 0.5X_1 + \epsilon/10, where ϵ∼N(0,1)\epsilon \sim N(0, 1)

  • Y=2+2X1+0.3X2+eY = 2 + 2X_1 + 0.3X_2 + e, where e∼N(0,1)e \sim N(0, 1)

(a) Simulate a data set with 100 observations of the three variables, and then answer the following questions using the simulated data.

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import pandas as pd

n = 100
X1 = np.random.uniform(0, 1, n)  # X1 ~ Uniform[0,1]
epsilon = np.random.normal(0, 1, n)  # ε ~ N(0,1)
X2 = 0.5 * X1 + epsilon / 10  # X2 = 0.5X1 + ε/10
e = np.random.normal(0, 1, n)  # e ~ N(0,1)
Y = 2 + 2 * X1 + 0.3 * X2 + e  # Y = 2 + 2X1 + 0.3X2 + e

data = pd.DataFrame({'X1': X1, 'X2': X2, 'Y': Y})

First 5 rows:

X1 X2 Y
0 0.374540 0.256819 3.154957
1 0.950714 0.404141 4.061275
2 0.731994 0.324143 3.672768
3 0.598658 0.342942 3.480679
4 0.156019 0.074980 2.567555

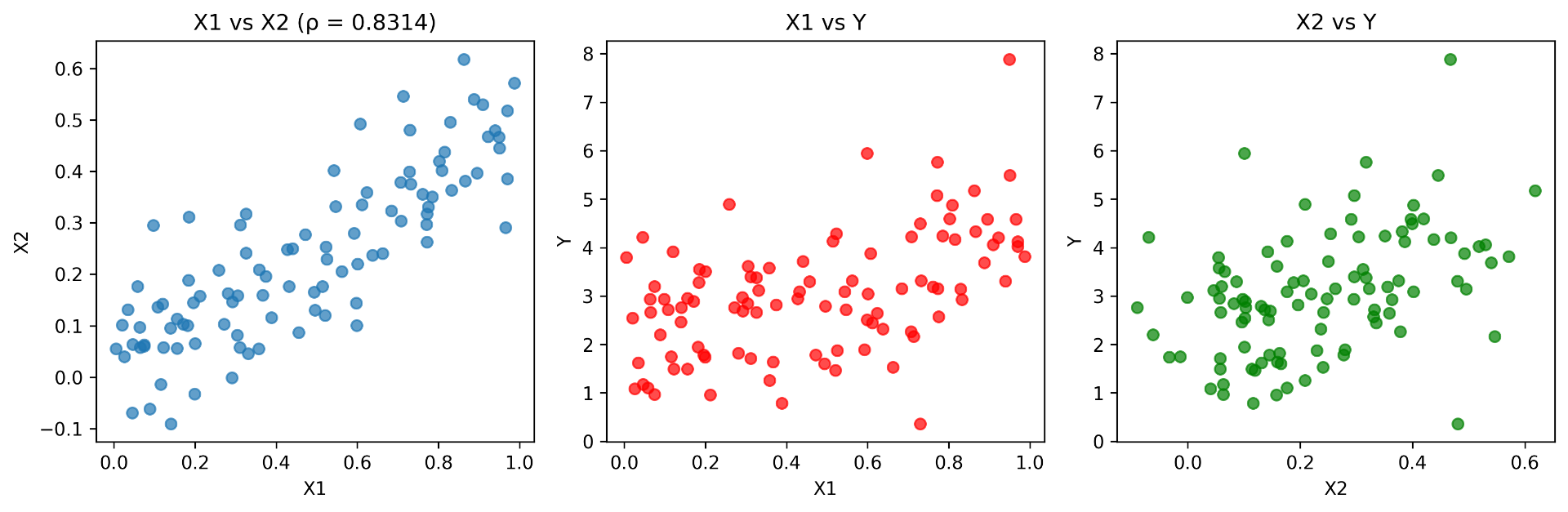
(b) What is the correlation between X1X_1 and X2X_2? Create a scatter plot displaying the relationship between the two variables.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import matplotlib.pyplot as plt

correlation = np.corrcoef(X1, X2)[0, 1]

plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.scatter(X1, X2, alpha=0.7)
plt.xlabel('X1')
plt.ylabel('X2')
plt.title(f'X1 vs X2 (ρ={correlation:.4f})')

plt.subplot(1, 3, 2)
plt.scatter(X1, Y, alpha=0.7, color='red')
plt.xlabel('X1')
plt.ylabel('Y')
plt.title('X1 vs Y')

plt.subplot(1, 3, 3)
plt.scatter(X2, Y, alpha=0.7, color='green')
plt.xlabel('X2')
plt.ylabel('Y')
plt.title('X2 vs Y')

plt.tight_layout()
plt.savefig('scatter_plots.png', dpi=300, bbox_inches='tight')
plt.show()

From the simulated data, we find:

ρX1,X2=Cov(X1,X2)σX1σX2≈0.8314>0.7\rho_{X_1, X_2} = \frac{\text{Cov}(X_1, X_2)}{\sigma_{X_1} \sigma_{X_2}} \approx 0.8314 \gt 0.7

This indicates a strong positive linear relationship.

scatter_plots.png

© Fit a least squares regression to predict YY using X1X_1 and X2X_2. Describe the results obtained. What are 0, 1, and 2? How do these relate to the true β0\beta_0, β1\beta_1, and β2\beta_2? Can you reject the null hypothesis H0:β1=0? How about the null hypothesis H0:β2=0H_0:\beta_2=0?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import scipy.stats as stats

X_multi = data[['X1', 'X2']]
model_multi = LinearRegression()
model_multi.fit(X_multi, Y)

y_pred_multi = model_multi.predict(X_multi)
r2_multi = r2_score(Y, y_pred_multi)

n = len(Y)
p = 2
adj_r2_multi = 1 - (1 - r2_multi) * (n - 1) / (n - p - 1)

residuals = Y - y_pred_multi
mse = np.sum(residuals**2) / (n - p - 1)
X_with_intercept = np.column_stack([np.ones(n), X_multi])
cov_matrix = mse * np.linalg.inv(X_with_intercept.T @ X_with_intercept)
se = np.sqrt(np.diag(cov_matrix))
t_stats = np.array([model_multi.intercept_] + list(model_multi.coef_)) / se
p_values = 2 * (1 - stats.t.cdf(np.abs(t_stats), n - p - 1))
````
Model: $Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \text{error}$

Estimates:
$$
\hat{\beta}_0 = 2.0381, \quad \hat{\beta}_1 = 2.1333, \quad \hat{\beta}_2 = 0.0282
$$

True: $\beta_0 = 2$, $\beta_1 = 2$, $\beta_2 = 0.3$

Hypothesis tests:
- $H_0: \beta_1 = 0$, p-value = 0.0021 $\to$ reject
- $H_0: \beta_2 = 0$, p-value = 0.9818 $\to$ fail to reject

$R^2 = 0.2530$, adjusted $R^2 = 0.2376$

### (d) Now fit a least squares regression to predict $Y$ using only $X_1$. Comment on your results. Can you reject the null hypothesis $H_0:\beta_1=0$0?

```python
X1_single = data[['X1']]
model_single1 = LinearRegression()
model_single1.fit(X1_single, Y)

y_pred_single1 = model_single1.predict(X1_single)
r2_single1 = r2_score(Y, y_pred_single1)

Model: Y=β0+β1X1+errorY = \beta_0 + \beta_1 X_1 + \text{error}

Estimates:

β^0=2.0387,β^1=2.1461\hat{\beta}_0 = 2.0387, \quad \hat{\beta}_1 = 2.1461

R2=0.2530R^2 = 0.2530. H0:β1=0H_0: \beta_1 = 0, p-value significant →\to reject.

(e) Now fit a least squares regression to predict YY using only X2X_2. Comment on your results. Can you reject the null hypothesis $H_0:\beta_1=0$0?

1
2
3
4
5
6
X2_single = data[['X2']]
model_single2 = LinearRegression()
model_single2.fit(X2_single, Y)

y_pred_single2 = model_single2.predict(X2_single)
r2_single2 = r2_score(Y, y_pred_single2)

Model: Y=β0+β1X2+errorY = \beta_0 + \beta_1 X_2 + \text{error}

Estimates:

β^0=2.2779,β^1=3.2763\hat{\beta}_0 = 2.2779, \quad \hat{\beta}_1 = 3.2763

R2=0.1758R^2 = 0.1758. H0:β1=0H_0: \beta_1 = 0, p-value significant →\to reject.

(f) Do the results obtained in ©-(e) contradict each other? Explain your answer.

No. Multicollinearity inflates standard errors in multiple regression, making β2\beta_2 insignificant. Simple regressions capture combined effects, so coefficients are significant.

(g) Now suppose we obtain one additional observation ((0.1, 0.8, 6)) (i.e., (x_1 = 0.1), (x_2 = 0.8), (y = 6)), which was unfortunately mismeasured. Please add this observation to the simulated data set and re-fit the linear models in ©-(e) using the new data. What effect does this new observation have on each model? In each model, is this observation an outlier (outlying Y observation)? Is it a high-leverage point (outlying X observation)? Or both? Explain your answer.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
new_row = pd.DataFrame({'X1': [0.1], 'X2': [0.8], 'Y': [6]})
new_data = pd.concat([data, new_row], ignore_index=True)

# Re-run multiple regression
X_multi_new = new_data[['X1', 'X2']]
Y_new = new_data['Y']
model_multi_new = LinearRegression()
model_multi_new.fit(X_multi_new, Y_new)

# Re-run simple regression Y~X1
model_single1_new = LinearRegression()
model_single1_new.fit(new_data[['X1']], Y_new)

# Re-run simple regression Y~X2
model_single2_new = LinearRegression()
model_single2_new.fit(new_data[['X2']], Y_new)

# Calculate VIF
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant

X_with_const = add_constant(X_multi)
vif_data = pd.DataFrame()
vif_data["Variable"] = ['const', 'X1', 'X2']
vif_data["VIF"] = [variance_inflation_factor(X_with_const.values, i) for i in range(X_with_const.shape[1])]

After adding point:

  • Multiple regression: β^0=2.0608\hat{\beta}_0 = 2.0608, β^1=1.1315\hat{\beta}_1 = 1.1315, β^2=2.0298\hat{\beta}_2 = 2.0298, R2=0.2425R^2 = 0.2425

  • Y∼X1Y \sim X_1: β^1=1.9918\hat{\beta}_1 = 1.9918

  • Y∼X2Y \sim X_2: β^1=3.4866\hat{\beta}_1 = 3.4866

This point is an outlier (high Y) and a high-leverage point (extreme X2). It has a greater impact on the multiple regression.