#sdsc5001

English / 中文

统计学与机器学习的术语对比

统计学 机器学习
分类/回归
聚类
含缺失响应的分类/回归
(非线性)降维		 监督学习
无监督学习
半监督学习
流形学习
协变量/响应变量
样本/总体
统计模型
误分类/预测误差		 特征/结果
训练集/测试集
学习器
泛化误差
多类逻辑函数
截断线性函数		 Softmax函数
ReLU(线性整流单元)

关键说明：两个领域使用不同术语描述相似概念，但核心思想相通。例如统计学的"协变量"对应机器学习的"特征"。

实际应用案例

工资预测案例

任务：理解员工工资与多个因素之间的关联关系

截屏2025-09-19 23.02.14.png

数据来源：基于美国大西洋地区男性员工收集的数据集

垃圾邮件检测案例

任务：构建能够自动检测垃圾邮件的过滤器

数据表示：

观测值 make% address% … 总大写字母数 是否为垃圾邮件
1 0 0.64 … 278 1(是)
2 0.21 0.28 … 1028 1(是)
3 0 0 … 7 0(否)
… … … … … …
4600 0.3 0 … 78 0(否)
4601 0 0 … 40 0(否)

数据集特征：

  • 4601封邮件，2个类别

  • 57个术语的频率特征

  • 简单分类函数：I(Capital_total>100)I(\text{Capital\_total} > 100)，其中I(⋅)I(\cdot)为指示函数

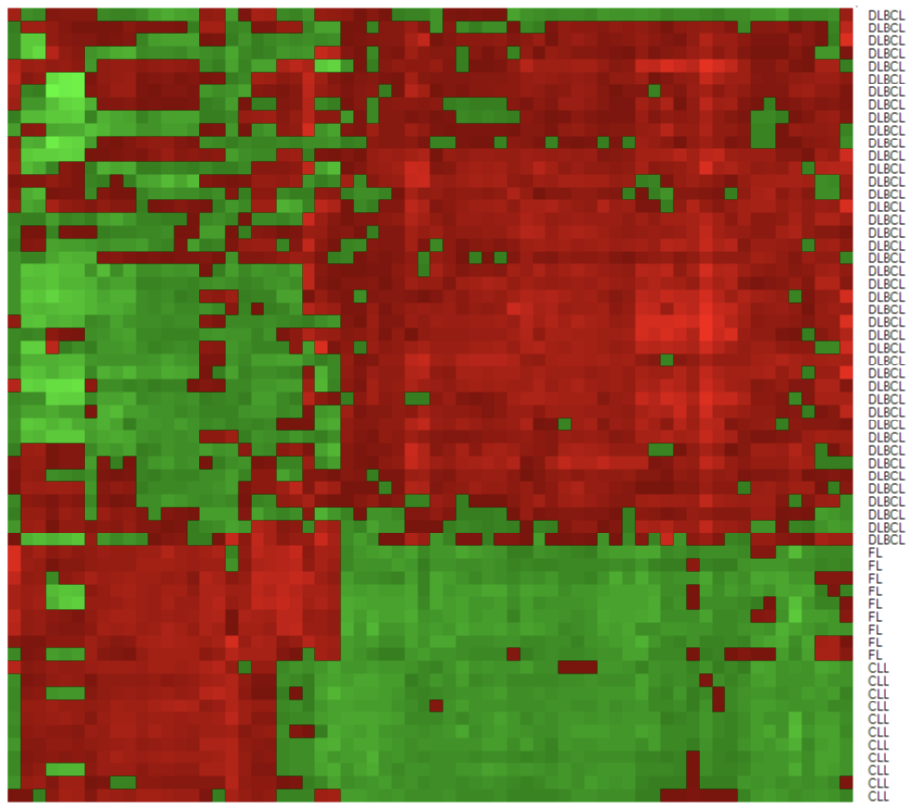
基因微阵列案例

任务：基于患者基因型自动诊断癌症
数据特征：

  • 4026个基因表达谱

  • 62名患者，3种成人淋巴恶性肿瘤类型

  • 66个"精心"选择的基因

截屏2025-09-19 23.04.31.png

基本符号表示

训练样本：(xi,yi)i=1n\left(x_{i}, y_{i}\right)_{i=1}^{n}

  • xix_{i}：输入、特征向量、预测变量、自变量，xi∈Rpx_i \in \mathbb{R}^p

  • yiy_i：输出、响应变量、因变量，为标量(也可为实向量)

数据生成模型：

Y=f(X)+ϵY = f(X) + \epsilon

  • ff：未知函数，表示X提供的关于Y的系统性信息

  • ϵ\epsilon：随机误差项，满足：

    • 均值为零：E(ϵ)=0\mathbb{E}(\epsilon)=0
    • 与X独立

误差项ϵ\epsilon存在的原因：

  1. 未测量的因素

  2. 测量误差

  3. 内在随机性

估计方法

参数模型

  • 线性/多项式回归模型

  • 广义线性回归模型

  • Fisher判别分析

  • 逻辑回归

  • 深度学习

非参数模型

  • 局部平滑

  • 平滑样条

  • 分类回归树、随机森林、提升方法

  • 支持向量机

预测与推断 (不考)

预测

基于估计函数f^\hat{f}，对新X预测响应：

Y^=f^(X)\widehat{Y} = \hat{f}(X)

预测误差分解：

E(Y^−Y)2=E(f^(X)−f(X))2⏟可减少误差+var⁡(ϵ)⏟不可减少误差\mathbb{E}(\widehat{Y}-Y)^{2} = \underbrace{\mathbb{E}(\hat{f}(X)-f(X))^{2}}_{\text{可减少误差}} + \underbrace{\operatorname{var}(\epsilon)}_{\text{不可减少误差}}

  • 可减少误差：可通过改进学习技术来减小

  • 不可减少误差：由于ϵ\epsilon无法用X预测，无法消除

推断

目标：理解Y如何受X影响

  • 哪些预测变量与Y相关？

  • Y与每个预测变量的关系如何？

  • 干预某些预测变量时Y如何变化？

预测与推断的平衡：

  • 简单模型(如线性模型)：解释性强但预测精度可能较低

  • 复杂非线性模型：预测精度高但解释性差

分类问题

分类与回归略有不同：

P(Y=k∣X)=fk(X);k=1,…,KP(Y=k \mid X)=f_{k}(X); \quad k=1,\ldots, K

分类决策函数：

ϕ^(X)=argmax⁡kf^k(X)\hat{\phi}(X) = \underset{k}{\operatorname{argmax}} \hat{f}_{k}(X)

误分类误差：

P(Y≠ϕ^(X))=E(I(Y≠ϕ^(X)))P(Y \neq \hat{\phi}(X)) = \mathbb{E}(I(Y \neq \hat{\phi}(X)))

示例：二分类玩具问题

问题描述：从未知分布模拟200个点，两个类别{蓝色, 橙色}各100个，构建预测规则

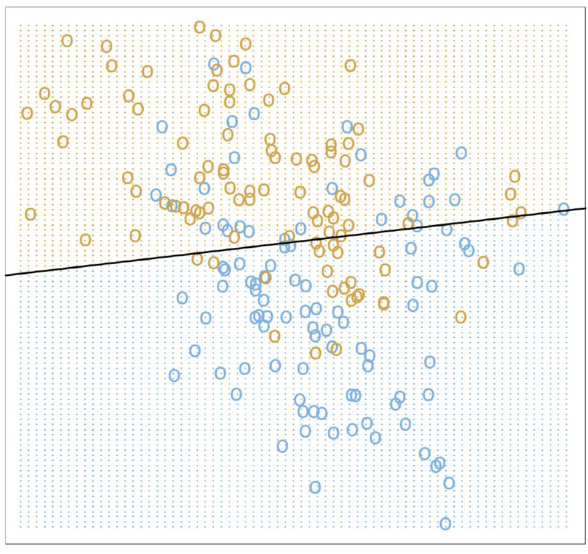
截屏2025-09-19 23.05.35.png

模型1：线性回归

编码：Y=1Y=1（橙色），Y=0Y=0（蓝色）

模型形式：

Y=β0+∑j=1pXjβj=XβY = \beta_0 + \sum_{j=1}^p X_j\beta_j = X\beta

参数估计（最小二乘）：

β^=(XTX)−1XTy\hat{\beta} = \left(X^{T} X\right)^{-1} X^{T} y

分类决策函数：

ϕ^(X)=I(XTβ^>0.5)\hat{\phi}(X) = I\left(X^T\hat{\beta} > 0.5\right)

模型2：K近邻(K-NN)

基于邻居预测：

y^(X)=1k∑i=1nyiI(xi∈Nk(X))\hat{y}(X) = \frac{1}{k}\sum_{i=1}^n y_i I\left(x_i \in N_k(X)\right)

其中Nk(X)N_k(X)是包含恰好k个邻居的X的邻域

分类决策函数（多数投票）：

ϕ^(X)=I(y^(X)>0.5)\widehat{\phi}(X) = I(\widehat{y}(X) > 0.5)

模型复杂度对比：

  • 线性回归：使用3个参数

  • K-NN分类器：使用n/kn/k个有效参数

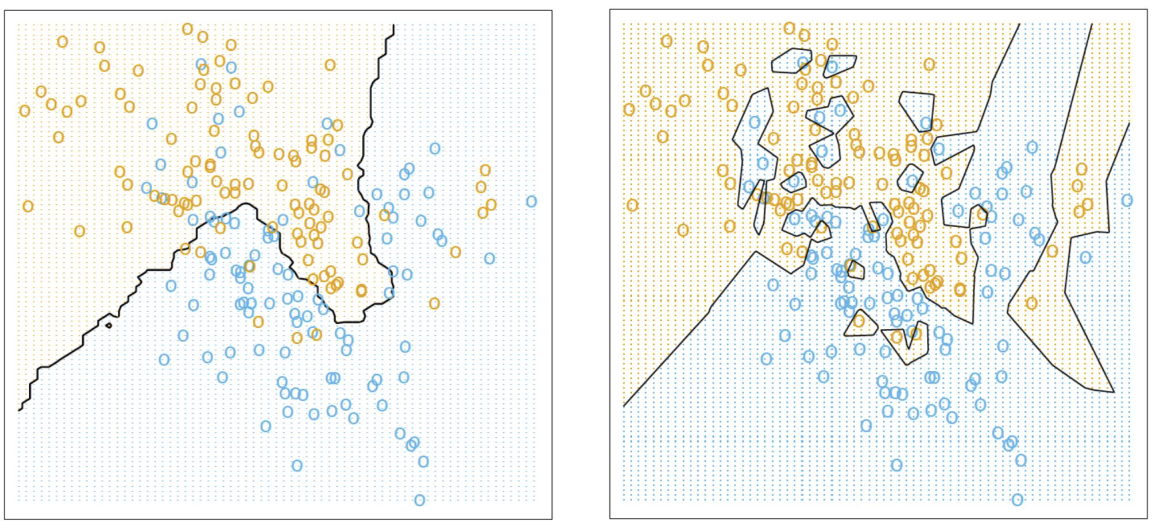
截屏2025-09-19 23.07.19.png

15-NN和1-NN分类结果对比图

回归模型评估

均方误差（MSE）及其最小化

均方误差（MSE）的定义

对于回归问题，其中 Y∈RY \in \mathbb{R} 和 X∈RpX \in \mathbb{R}^p，函数 ff 的准确性可以通过均方误差（Mean Square Error, MSE）来度量。MSE 定义为：

MSE⁡(f)=E[(Y−f(X))2]\operatorname{MSE}(f) = \mathbb{E}\left[(Y - f(X))^2\right]

其中，期望 E\mathbb{E} 是关于 XX 和 YY 的联合分布取的。MSE 衡量了预测值 f(X)f(X) 与真实值 YY 之间的平均平方差异，是评估预测模型性能的重要指标。

直观解释：MSE 越小，表示模型的预测越准确。它惩罚较大的误差更严重（由于平方项），因此对异常值敏感。

MSE 的最小化器

理论表明，MSE 的最小化器是条件期望函数：

f∗(X)=E[Y∣X]f^*(X) = \mathbb{E}[Y \mid X]

这意味着，当 f(X)f(X) 等于给定 XX 时 YY 的条件期望时，MSE 达到最小值。这个结果来自概率论中的条件期望性质：E[Y∣X]\mathbb{E}[Y \mid X] 是 YY 在给定 XX 下的最佳预测（在最小平方误差意义上）。

推导简要说明：

通过展开 MSE：

E[(Y−f(X))2]=E[(Y−E[Y∣X]+E[Y∣X]−f(X))2]\mathbb{E}[(Y - f(X))^2] = \mathbb{E}[(Y - \mathbb{E}[Y|X] + \mathbb{E}[Y|X] - f(X))^2]

利用条件期望的性质，可以证明：

E[(Y−f(X))2]=E[(Y−E[Y∣X])2]+E[(E[Y∣X]−f(X))2]\mathbb{E}[(Y - f(X))^2] = \mathbb{E}[(Y - \mathbb{E}[Y|X])^2] + \mathbb{E}[(\mathbb{E}[Y|X] - f(X))^2]

由于第一项是常数（与 ff 无关），最小化 MSE 等价于最小化第二项，即当 f(X)=E[Y∣X]f(X) = \mathbb{E}[Y|X] 时，第二项为零。

训练误差

在实践中，联合分布 (X,Y)(X, Y) 是未知的，因此我们不能直接计算理论上的 MSE。 相反，我们基于样本数据集来近似均方误差（MSE） {(xi,yi)}i=1n\{(x_i, y_i)\}_{i=1}^n.

MSE⁡^(f)=1n∑i=1n(yi−f(xi))2\widehat{\operatorname{MSE}}(f) = \frac{1}{n} \sum_{i=1}^{n} (y_i - f(x_i))^2

这被称为经验风险或训练误差。然而，需要注意的是：

  • 这个估计是对理论 MSE 的近似，但可能是有偏的，特别是如果模型过拟合训练数据。

  • 倾向于低估真实MSE，复杂模型可能获得极小的训练误差

测试误差

使用独立测试样本(x0i,y0i)i=1m\left(x_{0 i}, y_{0 i}\right)_{i=1}^{m}：

1m∑i=1m(y0i−f^(x0i))2\frac{1}{m}\sum_{i=1}^{m}\left(y_{0 i}-\hat{f}\left(x_{0 i}\right)\right)^{2}

优势：更接近真实MSE，模拟未来待预测的观测值

截屏2025-09-19 23.17.48.png

偏差-方差分解

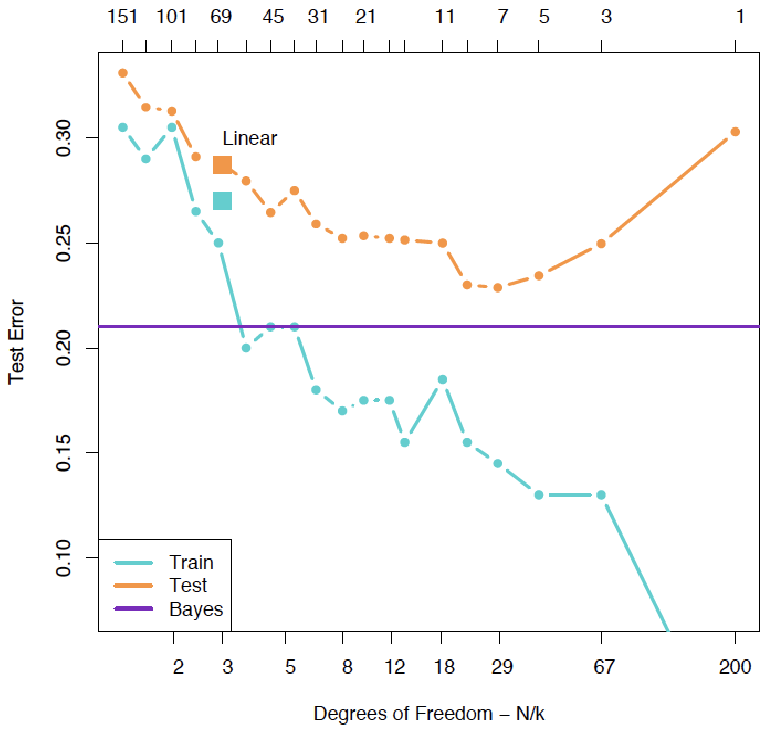
测试误差的U形曲线

测试误差随模型复杂度变化呈现典型的U形曲线，这是由两个相互竞争的量共同作用的结果：

E[(Y−f^(X))2]=E[(f^(X)−f(X))2]+var⁡(ε)=[Bias⁡(f^(X))]2+var⁡(f^(X))+var⁡(ε)\begin{align*} \mathbb{E}[(Y-\hat{f}(X))^2] = & \mathbb{E}[(\hat{f}(X)-f(X))^2] + \operatorname{var}(\varepsilon) \\ = & [\operatorname{Bias}(\hat{f}(X))]^2 + \operatorname{var}(\hat{f}(X)) + \operatorname{var}(\varepsilon) \end{align*}

关键说明：此分解揭示了预测误差的三个来源：偏差、方差和不可减少的误差。

偏差项

Bias⁡(f^(X))=E[f^(X)]−f(X)\operatorname{Bias}(\hat{f}(X)) = \mathbb{E}[\hat{f}(X)] - f(X)

  • 定义：估计值f^(X)\hat{f}(X)的期望与真实函数f(X)f(X)之间的差异

  • 含义：由于用f^\hat{f}近似ff而引入的系统性误差

  • 特点：反映了模型的拟合能力

方差项

var⁡(f^(X))=E[(f^(X)−E[f^(X)])2]\operatorname{var}(\hat{f}(X)) = \mathbb{E}[(\hat{f}(X)-\mathbb{E}[\hat{f}(X)])^2]

  • 定义：估计值f^(X)\hat{f}(X)在其期望周围的波动程度

  • 含义：如果使用不同的训练集估计f^\hat{f}，其值会发生多大变化

  • 特点：反映了模型对训练数据变化的敏感性

不可减少误差

var⁡(ε)\operatorname{var}(\varepsilon)

  • 定义：随机误差项ε\varepsilon的方差

  • 含义：由于数据内在随机性导致的误差，无法通过改进模型减少

  • 特点：为预测误差设定了理论下限

偏差-方差权衡

随着模型复杂度增加：

  • 偏差减小：复杂模型能更好地拟合数据中的复杂模式

  • 方差增加：复杂模型对训练数据中的噪声更敏感

这种权衡关系导致了测试误差的U形曲线：

  • 简单模型：高偏差，低方差（欠拟合）

  • 复杂模型：低偏差，高方差（过拟合）

  • 最优模型：在偏差和方差之间取得平衡

示例：在线性回归中，增加多项式特征可以降低偏差但会增加方差；正则化(如岭回归)可以减少方差但可能增加轻微偏差。

分类模型的评估

误分类误差 (Misclassification Error)

对于分类问题，其中 Y∈{1,…,K}Y \in \{1, \ldots, K\} 和 X∈RpX \in \mathbb{R}^p，函数 ff 的准确性可以通过误分类误差来度量：

MCE⁡(f)=E[I(Y≠f(X))]\operatorname{MCE}(f) = \mathbb{E}[I(Y \neq f(X))]

其中期望 E\mathbb{E} 是关于 XX 和 YY 的联合分布取的，I(⋅)I(\cdot) 是指示函数。

直观解释：误分类误差衡量的是模型做出错误分类的概率，是分类问题中最直接的性能度量指标。

贝叶斯规则 (Bayes Rule)

误分类误差的最小化器必须满足：

f∗(X)=arg⁡max⁡kP(Y=k∣X)f^{*}(X) = \underset{k}{\arg\max} P(Y=k \mid X)

这被称为贝叶斯规则或贝叶斯分类器，是在已知特征 XX 的情况下最优的分类决策。

推导说明：对于任意分类规则 ϕ(X)\phi(X)，其条件误分类误差为：

P(Y≠ϕ(X)∣X=x)=1−P(Y=ϕ(x)∣X=x)P(Y \neq \phi(X) \mid X = x) = 1 - P(Y = \phi(x) \mid X = x)

要最小化此概率，应选择 ϕ(x)\phi(x) 使得 P(Y=ϕ(x)∣X=x)P(Y = \phi(x) \mid X = x) 最大，即选择后验概率最大的类别。

训练误差与测试误差

训练误差

给定训练样本 {(xi,yi)}i=1n\{(x_i, y_i)\}_{i=1}^n 和估计函数 f^\hat{f}，其训练误差为：

1n∑i=1nI(yi≠f^(xi))\frac{1}{n} \sum_{i=1}^{n} I(y_i \neq \hat{f}(x_i))

特点：衡量模型在训练数据上的表现，但可能低估真实的误分类误差。

测试误差

如果有测试样本 {(x0i,y0i)}i=1m\{(x_{0i}, y_{0i})\}_{i=1}^m，则 f^\hat{f} 的测试误差为：

1m∑i=1mI(y0i≠f^(x0i))\frac{1}{m} \sum_{i=1}^{m} I(y_{0i} \neq \hat{f}(x_{0i}))

特点：提供模型在新数据上性能的无偏估计，是评估模型泛化能力的黄金标准。

截屏2025-09-19 23.30.35.png

交叉验证方法

验证集方法

优点：思想简单，易于实现
缺点：

  • 验证MSE可能高度可变

  • 仅使用部分观测值拟合模型，性能可能下降

留一法交叉验证(LOOCV)

步骤：

  1. 将大小为n的数据集分割为：训练集(n-1)和验证集(1)

  2. 使用训练集拟合模型

  3. 使用验证集验证模型，计算MSE

  4. 重复n次

  5. 计算平均MSE

优势：

  • 偏差较小（使用n-1个观测值）

  • 产生的MSE变异性较小

劣势：计算密集

K折交叉验证

步骤：

  1. 将训练样本分为A1,…,AKA_{1},\ldots, A_{K}（通常K=5或10）

  2. 对每个k，使用除AkA_k外的所有数据拟合模型f^−k(x)\hat{f}^{-k}(x)

  3. 在AkA_k上计算预测误差：

    Ek(f^)=∑i∈AkL(yi,f^−k(xi))2E_{k}(\hat{f}) = \sum_{i\in A_{k}} L\left(y_{i},\hat{f}^{-k}\left(x_{i}\right)\right)^{2}

  4. 计算CV误差：

    CV(f^)=1n∑k=1KEk(f^)CV(\hat{f}) = \frac{1}{n}\sum_{k=1}^{K} E_{k}(\hat{f})

注：此处应有交叉验证过程示意图(附件页码)

交叉验证方法比较

基于三个模拟示例的对比：

  • 蓝色：测试误差

  • 黑色：LOOCV

  • 橙色：10折CV

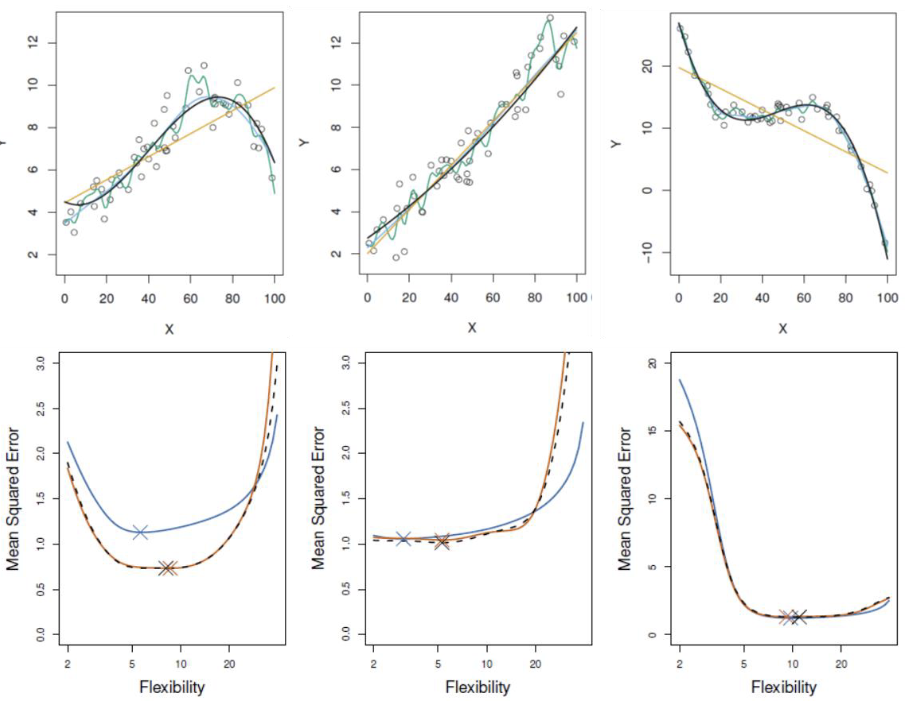
截屏2025-09-19 23.32.50.png

结论：

  • LOOCV比K折CV偏差小（当K<nK < n时）

  • LOOCV比K折CV方差高（当K<nK < n时）

  • 实践中通常使用K=5或10的K折CV

  • 经验表明K折CV能提供合理的测试误差估计