SDSC5001 课程 4-线性回归

#sdsc5001

English / 中文

Simple Linear Regression

基本设定

给定数据 $\left(x_{1}, y_{1}\right),\ldots,\left(x_{n}, y_{n}\right)$，其中：

• $x_{i} \in \mathbb{R}$ 是预测变量（自变量、输入、特征）

• $y_{i} \in \mathbb{R}$ 是响应变量（因变量、输出、结果）

回归函数表示为：

$$y = f(x) + \varepsilon$$

线性回归模型假设：

$$f(x) = \beta_0 + \beta_1 x$$

这通常被视为对真实关系的近似。

示例（附件页码2）：一个简单的玩具示例展示数据点和线性拟合关系。

最小二乘拟合

通过最小化残差平方和来估计参数：

$$\min_{\beta_0, \beta_1} \sum_{i=1}^{n} (y_i - (\beta_0 + \beta_1 x_i))^2$$

解为：

$$\begin{aligned} &\hat{\beta}_1 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}\\ &\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x} \end{aligned}$$

其中：

• $\hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_i$ 是拟合值

• $e_i = y_i - \hat{y}_i$ 是残差

参数估计与统计推断

模型假设

假设数据生成过程为：

$$Y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$$

其中 $\varepsilon_i$ 独立同分布于 $N(0, \sigma^2)$

在此假设下，可以证明：

• $\hat{\beta}_0$ 和 $\hat{\beta}_1$ 是 $\beta_0$ 和 $\beta_1$ 的无偏估计

  $$\hat{\beta}_1 \sim N\left(\beta_1,\frac{\sigma^2}{\sum_i(x_i - \bar{x})^2}\right)$$

• $\hat{\beta}_1$ 是所有无偏线性估计量中方差最小的（BLUE估计量）

  $$\hat{\beta}_0 \sim N\left(\beta_0,\left\{\frac{1}{n} + \frac{\bar{x}^2}{\sum_i(x_i - \bar{x})^2}\right\}\sigma^2\right)$$

无偏性的推导

为了证明 $\hat{\beta}_1$ 是无偏的，我们首先写出 $\hat{\beta}_1$ 的公式：

$$\hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}$$

其中 $\bar{x} = \frac{1}{n} \sum x_i$ 和 $\bar{y} = \frac{1}{n} \sum y_i$。

代入 $y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$，并注意到 $\bar{y} = \beta_0 + \beta_1 \bar{x} + \bar{\varepsilon}$，其中 $\bar{\varepsilon} = \frac{1}{n} \sum \varepsilon_i$。

经过代数简化（具体步骤略），可得：

$$\hat{\beta}_1 = \beta_1 + \frac{\sum (x_i - \bar{x}) \varepsilon_i}{\sum (x_i - \bar{x})^2}$$

取期望：

$$E[\hat{\beta}_1] = E\left[\beta_1 + \frac{\sum (x_i - \bar{x}) \varepsilon_i}{\sum (x_i - \bar{x})^2}\right] = \beta_1 + \frac{\sum (x_i - \bar{x}) E[\varepsilon_i]}{\sum (x_i - \bar{x})^2} = \beta_1$$

因为 $E[\varepsilon_i] = 0$。因此，$\hat{\beta}_1$ 是无偏的。

类似地，对于 $\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}$，取期望：

$$E[\hat{\beta}_0] = E[\bar{y}] - \bar{x} E[\hat{\beta}_1] = (\beta_0 + \beta_1 \bar{x}) - \bar{x} \beta_1 = \beta_0$$

所以 $\hat{\beta}_0$ 也是无偏的。

实际意义：无偏性意味着在多次重复抽样中，估计值的平均值会接近真实参数值，这增加了估计的可靠性。

BLUE性质的推导（高斯-马尔可夫定理）

高斯-马尔可夫定理指出，在线性回归模型中，如果误差项满足零均值、同方差且不相关，则最小二乘估计量 $\hat{\beta}_1$ 是所有线性无偏估计量中方差最小的。

考虑任何线性无偏估计量 $b_1 = \sum_{i} c_i y_i$，其中 $c_i$ 是常数。无偏性要求 $E[b_1] = \beta_1$，这 implies $\sum c_i = 0$ 和 $\sum c_i x_i = 1$（通过代入 $y_i$ 的表达式）。

方差为：

$$\text{Var}(b_1) = \text{Var}\left(\sum c_i y_i\right) = \sum c_i^2 \text{Var}(y_i) = \sigma^2 \sum c_i^2$$

因为 $\text{Var}(y_i) = \sigma^2$。

最小二乘估计量 $\hat{\beta}_1$ 的方差为：

$$\text{Var}(\hat{\beta}_1) = \frac{\sigma^2}{\sum (x_i - \bar{x})^2}$$

通过优化问题，可以证明对于任何其他线性无偏估计量 $b_1$，有 $\text{Var}(b_1) \geq \text{Var}(\hat{\beta}_1)$。这体现了 $\hat{\beta}_1$ 的最小方差性。

实际意义：BLUE性质意味着OLS估计量是最精确的（方差最小），从而在统计推断中更有效，例如构建置信区间时更窄。

举例说明

假设我们有一个简单的数据集：房屋面积（$x_i$）和房价（$y_i$）。模型为 $y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$。

• $\beta_0$ 可能表示当面积为0时的基础房价（但实际中可能没有意义，所以常被视为模型偏移）。

• $\beta_1$ 表示每增加一平方米，房价平均增加多少元。

• 无偏性：如果我们多次收集数据并计算 $\hat{\beta}_1$，其平均值会接近真实的 $\beta_1$。

• BLUE：如果我们使用其他线性方法（如加权最小二乘），但权重选择不当，方差可能会更大，导致估计不如OLS稳定。

置信区间

$\sigma^2$ 可由无偏的MSE估计：

$$\hat{\sigma}^2 = \text{MSE} = \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{n-2}$$

基于Cochran定理，$\hat{\beta}_0$ 和 $\hat{\beta}_1$ 的置信区间为：

$$\hat{\beta}_j \pm t\left(\frac{\alpha}{2}, n-2\right) \cdot \text{se}(\hat{\beta}_j), \quad j=0,1$$

符号定义与解释

• $\sigma^2$：误差项的方差，表示数据中无法由模型解释的变异程度。它是一个未知的常数参数。

• $\hat{\sigma}^2$ 或 MSE：均方误差（Mean Squared Error），是 $\sigma^2$ 的无偏估计量。计算公式为 $\hat{\sigma}^2 = \text{MSE} = \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{n-2}$，其中 $n$ 是样本大小，$n-2$ 是自由度（因为估计了两个参数 $\beta_0$ 和 $\beta_1$）。MSE 衡量了模型预测的平均误差平方。

• $\text{se}(\hat{\beta}_j)$：估计量 $\hat{\beta}_j$ 的标准误（standard error），表示 $\hat{\beta}_j$ 的抽样分布的标准差。对于简单线性回归，有：

  • $\text{se}(\hat{\beta}_0) = \sqrt{\text{MSE} \cdot \left( \frac{1}{n} + \frac{\bar{x}^2}{\sum_{i=1}^{n} (x_i - \bar{x})^2} \right)}$
  • $\text{se}(\hat{\beta}_1) = \sqrt{\frac{\text{MSE}}{\sum_{i=1}^{n} (x_i - \bar{x})^2}}$

• $t\left(\frac{\alpha}{2}, n-2\right)$：t 分布的上 $\alpha/2$ 分位数，其中 $\alpha$ 是显著性水平（例如，95% 置信水平对应 $\alpha=0.05$），$n-2$ 是自由度。t 分布用于当总体方差未知时，代替正态分布构建置信区间。

置信区间的推导原理

置信区间的推导基于以下步骤：

1. 抽样分布：在模型假设下（误差项 $\varepsilon_i \sim N(0, \sigma^2)$ 且独立），最小二乘估计量 $\hat{\beta}_j$ 服从正态分布：

   $$\hat{\beta}_j \sim N\left(\beta_j, \text{Var}(\hat{\beta}_j)\right)$$

   其中 $\text{Var}(\hat{\beta}_j)$ 是方差，取决于 $\sigma^2$。

2. 方差估计：由于 $\sigma^2$ 未知，我们使用 MSE 来估计它。Cochran 定理（或相关定理）确保：

   • $\hat{\sigma}^2 = \text{MSE}$ 与 $\hat{\beta}_j$ 独立。
   • $\frac{(n-2) \text{MSE}}{\sigma^2} \sim \chi^2(n-2)$，即服从自由度为 $n-2$ 的卡方分布。

3. t 统计量：将 $\hat{\beta}_j$ 标准化后，得到 t 统计量：

   $$t = \frac{\hat{\beta}_j - \beta_j}{\text{se}(\hat{\beta}_j)} \sim t(n-2)$$

   这是因为：

   $$t = \frac{\hat{\beta}_j - \beta_j}{\sqrt{\text{Var}(\hat{\beta}_j)}} \bigg/ \sqrt{\frac{\text{MSE}}{\sigma^2}} = \frac{N(0,1)}{\sqrt{\chi^2_{n-2} / (n-2)}}$$

   这正好是 t 分布的定义。

4. 置信区间：根据 t 分布的性质，有：

   $$P\left( -t_{\alpha/2, n-2} \leq \frac{\hat{\beta}_j - \beta_j}{\text{se}(\hat{\beta}_j)} \leq t_{\alpha/2, n-2} \right) = 1 - \alpha$$

   重新排列不等式，得到置信区间：

   $$\hat{\beta}_j \pm t_{\alpha/2, n-2} \cdot \text{se}(\hat{\beta}_j)$$

   这表示有 $1-\alpha$ 的置信度认为真实参数 $\beta_j$ 落在这个区间内。

实际意义与解释

置信区间提供了参数估计的不确定性度量。例如，对于 $\beta_1$ 的 95% 置信区间：

• 解释：如果我们重复抽样多次，每次计算一个置信区间，那么大约 95% 的这些区间会包含真实的 $\beta_1$。

• 应用：如果置信区间包含零，可能表示该预测变量对响应变量没有显著影响（但需假设检验确认）。区间宽度反映了估计的精度：区间越窄，估计越精确。

• 例子：在房价预测模型中，如果 $\beta_1$ 表示面积对房价的影响，其 95% 置信区间为 [100, 200]，则我们可以说“有 95% 的置信度认为，每增加一平方米，房价平均增加 100 到 200 元”。

举例说明

假设我们有一个简单线性回归模型，预测考试成绩（$y$）基于学习时间（$x$）。样本大小 $n=20$，计算得：

• $\hat{\beta}_1 = 5$（学习时间每增加一小时，成绩平均提高 5 分）

• $\text{se}(\hat{\beta}_1) = 0.8$

• $\text{MSE} = 10$，自由度 $n-2=18$

• 对于 95% 置信区间，$\alpha=0.05$，查 t 分布表得 $t_{0.025, 18} \approx 2.101$

则 $\beta_1$ 的置信区间为：

$$5 \pm 2.101 \times 0.8 = [3.32, 6.68]$$

这意味着我们有 95% 的置信度认为，真实的学习时间效应介于 3.32 到 6.68 分之间。

假设检验

检验 $H_0: \beta_1 = 0$ vs $H_1: \beta_1 \neq 0$：

$$t_1^* = \frac{\hat{\beta}_1}{\text{se}(\hat{\beta}_1)} \sim t_{n-2}$$

如果 $|t_1^*| > t\left(\frac{\alpha}{2}, n-2\right)$，拒绝 $H_0$

示例：拟合线和置信带

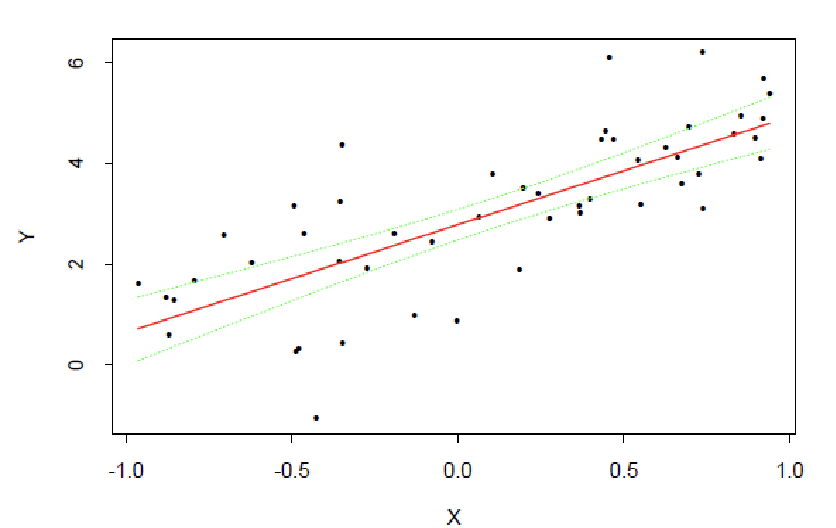
多元线性回归

模型设定

$$y_i = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i$$

矩阵形式：

$$\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}$$

其中：

• $\mathbf{y}$ 是 $n \times 1$ 响应向量

• $\mathbf{X}$ 是 $n \times (p+1)$ 设计矩阵（第一列为1）

• $\boldsymbol{\beta}$ 是 $(p+1) \times 1$ 参数向量

---

最小二乘估计

目标函数

最小二乘法的目标是最小化残差平方和：

$$\begin{aligned} \hat{\beta} & = \argmin_{\boldsymbol{\beta}} \sum_{i=1}^{n} \left(y_i - \beta_0 - \sum_{j=1}^{p} \beta_j x_{ji}\right)^2 \\ & = \argmin_{\boldsymbol{\beta}} (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^\top(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}) \end{aligned}$$

公式意义：左边是残差平方和的求和形式，右边是矩阵形式。$\mathbf{y}$ 是响应向量，$\mathbf{X}$ 是设计矩阵，$\boldsymbol{\beta}$ 是待估参数向量。

最小二乘解

通过求解上述优化问题，得到参数估计量：

$$\hat{\boldsymbol{\beta}} = (\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{y}$$

统计性质：

• 期望：$\mathbb{E}[\hat{\boldsymbol{\beta}}] = \boldsymbol{\beta}$（无偏估计）
• 协方差矩阵：$\text{cov}(\hat{\boldsymbol{\beta}}) = \sigma^2 (\mathbf{X}^\top\mathbf{X})^{-1}$

拟合值与帽子矩阵

拟合值计算

利用参数估计量得到拟合值：

$$\hat{\mathbf{y}} = \mathbf{X}\hat{\boldsymbol{\beta}} = \mathbf{X}(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{y} = \mathbf{H}\mathbf{y}$$

其中 $\mathbf{H} = \mathbf{X}(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top$ 称为帽子矩阵。

帽子矩阵性质：

• $\mathbf{H}$ 是对称幂等矩阵（$\mathbf{H}^2 = \mathbf{H}$）
• 迹 $\text{tr}(\mathbf{H}) = p + 1$（参数个数）
• 将响应向量 $\mathbf{y}$ 投影到设计矩阵的列空间

拟合值的统计性质

$$\mathbb{E}[\hat{\mathbf{y}}] = \mathbf{X}\boldsymbol{\beta}\\ \text{cov}(\hat{\mathbf{y}}) = \sigma^2\mathbf{H}$$

几何解释：拟合值 $\hat{\mathbf{y}}$ 是 $\mathbf{y}$ 在设计矩阵列空间上的正交投影。

残差性质分析

残差定义与表达式

残差向量定义为观测值与拟合值之差：

$$\mathbf{e} = \mathbf{y} - \hat{\mathbf{y}} = (\mathbf{I} - \mathbf{H})\mathbf{y}$$

残差的统计特性

$$\mathbb{E}[\mathbf{e}] = \mathbf{0}\\ \text{cov}(\mathbf{e}) = \sigma^2(\mathbf{I} - \mathbf{H})$$

关键理解：

• 残差的期望为零，说明模型无系统偏差
• 残差的协方差矩阵不是对角阵，说明不同观测的残差之间存在相关性
• $\mathbf{I} - \mathbf{H}$ 也是对称幂等矩阵，迹为 $n - p - 1$

残差平方和的期望

残差平方和的期望值推导：

$$\mathbb{E}[\mathbf{e}^\top\mathbf{e}] = \mathbb{E}[\text{tr}(\mathbf{e}^\top\mathbf{e})] = \mathbb{E}[\text{tr}(\mathbf{e}\mathbf{e}^\top)] = \text{tr}(\mathbb{E}[\mathbf{e}\mathbf{e}^\top]) \\ = \text{tr}(\sigma^2(\mathbf{I} - \mathbf{H})) = \sigma^2(n - p - 1)$$

推导说明：

• 利用迹的循环置换性质：$\text{tr}(ABC) = \text{tr}(BCA)$
• $\mathbb{E}[\mathbf{e}\mathbf{e}^\top] = \text{cov}(\mathbf{e}) = \sigma^2(\mathbf{I} - \mathbf{H})$
• $\text{tr}(\mathbf{H}) = p + 1$，因此 $\text{tr}(\mathbf{I} - \mathbf{H}) = n - (p + 1)$

方差估计

均方误差（MSE）

利用残差平方和估计误差方差：

$$\hat{\sigma}^2 = MSE = \frac{\mathbf{e}^\top\mathbf{e}}{n - p - 1}$$

统计意义：

• 分母 $n - p - 1$ 是残差的自由度
• 根据上述推导，$\mathbb{E}[\hat{\sigma}^2] = \sigma^2$，是无偏估计
• 用于衡量模型的拟合优度和进行统计推断

模型评估

ANOVA分解

总平方和分解

在回归分析中，总变异可以分解为回归解释的变异和残差变异：

$$SS_{TO} = SS_E + SS_R$$

其中：

• $SS_{TO}$：总平方和（Total Sum of Squares）

• $SS_E$：误差平方和（Error Sum of Squares）

• $SS_R$：回归平方和（Regression Sum of Squares）

矩阵形式表达

总平方和：

$$SS_{TO} = \mathbf{y}^T\left(\mathbf{I} - \frac{\mathbf{J}}{n}\right)\mathbf{y}$$

误差平方和：

$$SS_E = \mathbf{e}^T\mathbf{e} = \mathbf{y}^T(\mathbf{I} - \mathbf{H})\mathbf{y} = \mathbf{y}^T\mathbf{y} - \hat{\boldsymbol{\beta}}^T\mathbf{X}^T\mathbf{y}$$

回归平方和：

$$SS_R = \mathbf{y}^T\left(\mathbf{H} - \frac{\mathbf{J}}{n}\right)\mathbf{y} = \hat{\boldsymbol{\beta}}^T\mathbf{X}^T\mathbf{y} - \frac{(\sum y_i)^2}{n}$$

符号说明：

• $\mathbf{J}$ 是全1矩阵（$n \times n$，所有元素为1）
• $\mathbf{H}$ 是帽子矩阵 $\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T$
• $\mathbf{I}$ 是单位矩阵

期望值推导

误差平方和的期望

$$\mathbb{E}[SS_E] = \sigma^2(n - p - 1)$$

推导说明：由于 $\mathbb{E}[\mathbf{e}^T\mathbf{e}] = \sigma^2(n - p - 1)$，且 $SS_E = \mathbf{e}^T\mathbf{e}$

总平方和的期望

$$\mathbb{E}[SS_{TO}] = (n - 1)\sigma^2 + \boldsymbol{\beta}^T\mathbf{X}^T\left(\mathbf{I} - \frac{\mathbf{J}}{n}\right)\mathbf{X}\boldsymbol{\beta}$$

统计意义：

• $(n - 1)\sigma^2$：随机误差造成的变异

• $\boldsymbol{\beta}^T\mathbf{X}^T(\mathbf{I} - \frac{\mathbf{J}}{n})\mathbf{X}\boldsymbol{\beta}$：模型解释的系统性变异

回归平方和的期望

$$\mathbb{E}[SS_R] = p\sigma^2 + \boldsymbol{\beta}^T\mathbf{X}^T\left(\mathbf{I} - \frac{\mathbf{J}}{n}\right)\mathbf{X}\boldsymbol{\beta}$$

统计意义：

• $p\sigma^2$：由于参数估计不确定性带来的变异

• $\boldsymbol{\beta}^T\mathbf{X}^T(\mathbf{I} - \frac{\mathbf{J}}{n})\mathbf{X}\boldsymbol{\beta}$：真实回归效应解释的变异

决定系数

$$R^2 = \frac{SS_R}{SS_{TO}} = 1 - \frac{SS_E}{SS_{TO}}$$

衡量模型解释的变异比例，取值范围为[0,1]。

调整决定系数

$$R^2_{adj} = 1 - \frac{SS_E/(n-p-1)}{SS_{TO}/(n-1)}$$

考虑参数个数后的调整指标，用于比较不同复杂度的模型。

实际应用：ANOVA分析不仅提供模型整体显著性的检验，还为模型比较和选择提供重要依据。通过分解不同来源的变异，可以更好地理解模型的解释能力和拟合效果。

决定系数（$R^2$）与调整决定系数

决定系数 $R^2$

决定系数（系数 of multiple determination）定义为：

$$R^2 = \frac{SS_R}{SS_{TO}} = 1 - \frac{SS_E}{SS_{TO}}$$

统计意义：

• 衡量因变量Y的总变异中被预测变量X解释的比例

• 取值范围为[0,1]，值越大表示模型拟合越好

• 反映模型对数据的解释能力

示例：如果$R^2 = 0.85$，表示85%的Y变异可以被X解释，只有15%是随机误差。

$R^2$的局限性

$R^2$不适合用于比较不同模型，因为：

• 总是随着模型中变量数量的增加而增加

• 即使添加不相关的变量，$R^2$也不会减小

• 可能导致过拟合问题

调整决定系数 $R^2_a$

为了解决$R^2$的局限性，引入调整决定系数：

$$R_a^2 = 1 - \frac{SS_E/(n-p-1)}{SS_{TO}/(n-1)} = 1 - \frac{n-1}{n-p-1} \cdot \frac{SS_E}{SS_{TO}}$$

优势：

• 对变量个数进行惩罚，避免过度拟合

• 更适合比较不同复杂度的模型

• 只有当新变量对模型的改进足够大时，$R^2_a$才会增加

比较规则：在模型比较中，应优先选择$R^2_a$较大的模型。

线性模型的F检验

假设检验设置

检验整个回归模型的显著性：

$$H_0: \beta_1 = \beta_2 = \cdots = \beta_p = 0$$

$$H_a: \text{至少有一个} \beta_k \neq 0 \quad (k \geq 1)$$

原假设含义：所有斜率系数同时为0，即预测变量对响应变量没有线性影响。

F检验统计量

$$F^* = \frac{MS_R}{MS_E} = \frac{SS_R/p}{SS_E/(n-p-1)}$$

统计分布：在原假设成立条件下，$F^* \sim F(p, n-p-1)$

决策规则：如果$F^* > F(\alpha; p, n-p-1)$，则拒绝原假设。

实际应用：F检验用于判断回归模型是否整体显著。如果拒绝H₀，说明至少有一个预测变量对响应变量有显著的线性影响。

回归系数的统计推断

系数估计的协方差矩阵

理论协方差矩阵：

$$\text{cov}(\hat{\boldsymbol{\beta}}) = \sigma^2 (\mathbf{X}^T\mathbf{X})^{-1}$$

估计的协方差矩阵（用MSE代替未知的σ²）：

$$s^2(\hat{\boldsymbol{\beta}}) = MSE \cdot (\mathbf{X}^T\mathbf{X})^{-1}$$

单个系数的t检验

假设检验：

$$H_0: \beta_k = 0, \quad H_a: \beta_k \neq 0$$

检验统计量：

$$t^* = \frac{\hat{\beta}_k - \beta_k}{s(\hat{\beta}_k)} \sim t(n - p - 1); k = 0, \dots, p$$

其中$s(\hat{\beta}_k)$是$s(\hat{\beta})$矩阵中相应的对角线元素（系数标准误）。

统计分布：在正态误差假设下，$t^* \sim t(n-p-1)$

决策规则：如果$|t^*| > t(\alpha/2, n-p-1)$，则拒绝H₀。

置信区间构造

$\beta_k$的$100(1-\alpha)\%$置信区间：

$$\hat{\beta}_k \pm t\left(\frac{\alpha}{2}, n-p-1\right) \cdot s(\hat{\beta}_k)$$

实际应用示例

模型整体显著性检验

假设我们有p=3个预测变量，n=30个观测值：

• 计算得到$F^* = 15.2$

• 查F分布表：$F(0.05; 3, 26) ≈ 2.98$

• 由于$15.2 > 2.98$，拒绝H₀，模型整体显著

单个变量显著性检验

检验第二个预测变量的显著性：

• $\hat{\beta}_2 = 2.5$, $s(\hat{\beta}_2) = 0.8$

• $t^* = 2.5/0.8 = 3.125$

• $t(0.025, 26) ≈ 2.056$

• 由于$3.125 > 2.056$，$\beta_2$显著不为0

置信区间计算

$\beta_2$的95%置信区间：

• $2.5 \pm 2.056 \times 0.8 = [0.855, 4.145]$

模型诊断

正态误差假设模型回顾

线性回归模型的基本形式：

$$y_i = \beta_0 + \sum_{j=1}^{p} \beta_j x_{ij} + \varepsilon_i, \quad i = 1, \ldots, n$$

模型假设：

1. $\beta_0, \ldots, \beta_p$ 是待估参数

2. $x_i$ 被视为固定常数（非随机变量）

3. $\varepsilon_i$ 独立同分布于 $N(0, \sigma^2)$

潜在问题与模型不适用性

线性回归模型可能不适用的情况包括：

1. 回归函数非线性：真实关系不是线性形式

2. 遗漏重要预测变量：模型缺少关键解释变量

3. 误差方差异常：$\varepsilon$ 的方差非常数（异方差性）

4. 误差项不独立：$\varepsilon$ 之间存在自相关

5. 误差非正态分布：$\varepsilon$ 不服从正态分布

6. 异常值存在：少数极端观测值影响模型

7. 预测变量相关：多重共线性问题

残差性质与诊断基础

残差的定义与性质

残差是误差项的估计：$e_i = y_i - \hat{y}_i$

统计性质：

• $\mathbf{e} \sim N(0, \sigma^2(\mathbf{I} - \mathbf{H}))$

• 即使$\varepsilon_i$独立，$e_i$也不独立（但大样本下近似独立）

• $\mathbb{E}[e_i] = 0$, $\text{Var}(e_i) = \sigma^2(1 - h_{ii})$

标准化残差

为更好地诊断模型，常使用标准化残差：

半学生化残差：

$$e_i^* = \frac{e_i}{\sqrt{MSE}}$$

学生化残差（更常用）：

$$r_i = \frac{e_i}{\sqrt{MSE(1 - h_{ii})}}$$

注：学生化残差考虑了每个观测点的杠杆效应，更适合异常值检测。

回归函数非线性检测

诊断方法

1. 绘制残差与拟合值散点图

   • 如果关系为线性，残差应随机分布在0附近
   • 如果存在非线性模式，残差会显示系统性趋势

2. 绘制残差与预测变量散点图

   • 检查每个预测变量与残差的关系
   • 系统性模式表明该变量的函数形式不正确

线性回归模型诊断与问题处理

遗漏重要预测变量的诊断与处理

诊断方法

通过绘制残差与其他预测变量的散点图来检测：

• 如果残差与某个未包含的预测变量存在系统性模式，表明该变量应该被纳入模型

• 残差中出现的任何非随机模式都可能暗示遗漏了重要变量

变量选择问题

当存在多个预测变量时，变量选择成为一个重要研究领域：

• 前向选择：从空模型开始，逐步添加显著变量

• 后向消除：从全模型开始，逐步移除不显著变量

• 逐步回归：结合前向和后向方法

• 正则化方法：LASSO、岭回归等

实践建议：变量选择应基于理论指导和统计准则（如AIC、BIC）相结合

异方差性（误差方差异常）检测

诊断方法

检查残差与拟合值的散点图（附件页码25）：

• 理想情况下，所有残差应有大致相同的变异性

• 残差变异性随拟合值增加而增加（或减少）表明异方差性

• 由于残差符号对检测异方差性意义不大，常使用$|e_i|$或$e_i^2$与$\hat{y_i}$的散点图

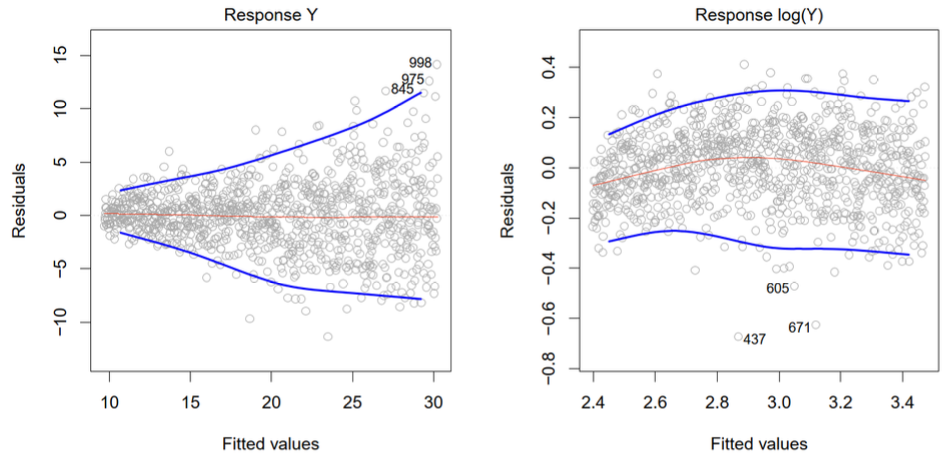
异方差性的影响

• 参数估计仍无偏，但标准误估计有偏

• t检验和F检验失效

• 置信区间和预测区间不准确

模型诊断：误差项检验

误差项的依赖性（Dependence of Error Terms）

在时间序列或空间数据中，需要检查残差 $e_i$ 与时间或地理位置的散点图：

• 目的：检测序列中相邻残差之间是否存在相关性

• 方法：绘制 $e_i$ 随时间或空间位置的散点图

• 理想情况：残差应随机分布，无特定模式

误差项的非正态性（Non-normality of Error Term）

检验残差 $e_i$ 正态性的三种方法：

1. 分布图（Distribution Plots）

   • 直方图：观察分布形状是否接近钟形曲线
   • 箱线图：检测对称性和异常值
   • 茎叶图：详细展示数据分布特征

2. 累积分布函数比较

   • 样本频率估计累积分布函数
   • 与理论正态分布的累积分布函数进行比较
   • 偏差较大表明非正态性

3. Q-Q 图（分位数-分位数图）

   • 原理：比较样本分位数与理论正态分布分位数
   • 判断标准：
     • 点近似落在直线上 → 支持正态性假设
     • 点明显偏离直线 → 误差项非正态分布
   • 优势：对正态性偏离敏感，可视化效果好

模型诊断的核心是验证线性回归的基本假设是否成立，特别是误差项 $\epsilon_i$ 的独立同分布和正态性假设。这些诊断工具帮助识别模型缺陷，为模型改进提供方向。

异常观测值（Outlying Observations）

定义

• 异常点：与大多数数据明显分离的观测值

• 分类：

  • 异常Y观测值（离群点）：$y_i$ 远离模型预测值
  • 异常X观测值（高杠杆点）：具有异常X值的观测点

异常Y观测值的检测方法

残差类型及其定义

1. 普通残差与半学生化残差

• 普通残差：$e_i = y_i - \hat{y}_i$

• 半学生化残差：$e_i^* = \frac{e_i}{\sqrt{MSE}}$

2. 学生化残差

• 定义：$r_i = \frac{e_i}{s(e_i)} = \frac{e_i}{\sqrt{MSE(1-h_{ii})}}$

• 特点：考虑了残差的变异性差异

3. 删除残差（Deleted Residual）

• 定义：$d_i = y_i - \hat{y}_{i(-i)}$

  • $\hat{y}_{i(-i)}$：不使用第i个观测值拟合的模型预测值

• 性质：$d_i = \frac{e_i}{1-h_{ii}}$

• 意义：模拟新观测值的预测误差

4. 学生化删除残差

• 定义：$t_i = \frac{d_i}{s(d_i)} = \frac{e_i}{\sqrt{MSE_{(-i)}(1-h_{ii})}}$

• 分布：$t_i \sim t_{n-p-2}$

• 计算公式：$t_i = e_i \left[ \frac{n-p-2}{SSE(1-h_{ii}) - e_i^2} \right]^{1/2}$

正式检验方法

• 检验统计量：比较 $|t_i|$ 与 $t(1-\frac{\alpha}{2n}, n-p-2)$

• Bonferroni校正：调整显著性水平以考虑多重检验

异常X观测值的检测

杠杆值（Leverage）

• 定义：帽子矩阵 $H = X(X^TX)^{-1}X^T$ 的对角元素 $h_{ii}$

• 性质：

  • $0 \leq h_{ii} \leq 1$
  • $\sum_{i=1}^n h_{ii} = tr(H) = p+1$

• 意义：衡量 $x_i$ 与所有X值中心的距离

• 判断标准：$h_{ii} > \frac{2(p+1)}{n}$ 表明异常X观测值

异常观测值检测是模型诊断的重要环节。离群点（Y异常）可能由测量误差引起，而高杠杆点（X异常）可能对回归结果产生过度影响。通过不同的残差定义和杠杆值分析，可以系统性地识别和处理这些异常点，提高模型的稳健性。

多重共线性（Multicollinearity）

定义与例子

• 多重共线性：预测变量之间存在高度相关性

• 理想情况：预测变量相互独立（统计中的"自变量"）

• 例子：

  • $Y \sim X_1(\text{weight}) + X_2(BMI) + \text{others}$
  • $Y \sim X_1(\text{credit rating}) + X_2(\text{credit limit}) + \text{others}$

多重共线性的影响

• 回归系数估计的方差变得非常大

• 删除一个变量后，回归系数可能改变符号

• 预测变量的边际显著性高度依赖于模型中包含的其他预测变量

• 预测变量的显著性可能被模型中相关变量掩盖

方差膨胀因子（VIF）

• 定义：$(\text{VIF})_j = (1 - R_j^2)^{-1}$

  • 其中 $R_j^2$ 是将第 $j$ 个变量对模型中其他 $p-1$ 个变量进行回归得到的决定系数

• 判断标准：

  • 最大VIF值超过10 → 认为多重共线性对最小二乘估计有不适当影响
  • 所有VIF的平均值远大于1 → 表明存在严重多重共线性

变量变换

目的

• 线性化非线性回归函数

• 稳定误差方差

• 使误差项正态化

Box-Cox变换

• 变换形式：使用 $y^\lambda$（$\lambda \geq 0$）作为响应变量，其中 $y^0$ 定义为 $\ln(Y)$

• 选择最优$\lambda$：基于最大化似然函数

  $$L(\lambda; \beta_0, \beta_1, \sigma^2) = \frac{1}{(2\pi\sigma)^{n/2}} \exp\left(-\frac{1}{2\sigma^2} \sum_{i=1}^n \left(y_i^{(\lambda)} - \beta_0 - \beta_1^T \mathbf{x}_i\right)^2\right)$$

偏差-方差权衡（Bias-Variance Tradeoff）

均方误差（MSE）分解

• 令 $f_0(\mathbf{x})$ 为 $\mathbf{x}$ 处的真实回归函数，则估计量 $\hat{f}(\mathbf{x})$ 的均方误差为：

  $$MSE(\hat{f}(\mathbf{x})) = E\left[ \left( \hat{f}(\mathbf{x}) - f_0(\mathbf{x}) \right)^2 \right]$$

• 分解为：

  $$MSE(\hat{f}(\mathbf{x})) = \text{var}(\hat{f}(\mathbf{x})) + \left[ E(\hat{f}(\mathbf{x})) - f_0(\mathbf{x}) \right]^2$$

  • 第一项：方差（估计量的波动性）
  • 第二项：偏差的平方（估计量的系统误差）

权衡关系与正则化

• 高斯-马尔可夫定理：如果线性模型正确，最小二乘估计 $\hat{f}$ 是无偏的，且在 $y$ 的所有线性无偏估计量中方差最小

• 有偏估计的优势：可能存在MSE更小的有偏估计量

• 正则化方法：通过正则化减小方差，如果偏差增加很小则值得

  • 子集选择（前向、后向、全子集）
  • 岭回归（Ridge Regression）
  • Lasso回归

• 现实情况：模型几乎从不完全正确，"最佳"线性模型与真实回归函数之间存在模型偏差

多重共线性会严重影响回归系数的解释和稳定性，需要通过VIF等指标检测。变量变换是改善模型假设的有效手段。偏差-方差权衡是模型选择的核心问题，正则化方法通过引入偏差来减小方差，可能获得更小的预测误差。

定性预测变量（Qualitative Predictors）

基本模型设定

考虑一个定量预测变量 $X_1$ 和一个有两个水平 $M_1$ 和 $M_2$ 的定性预测变量：

虚拟变量编码

• 定义：$X_2 = \begin{cases} 1 & \text{if level } M_1 \\ 0 & \text{if level } M_2 \end{cases}$

• 回归模型：$E(Y|X) = \beta_0 + \beta_1X_1 + \beta_2X_2$

模型解释

• 对于水平 $M_1$：$E(Y|X) = \beta_0 + \beta_1X_1 + \beta_2$

• 对于水平 $M_2$：$E(Y|X) = \beta_0 + \beta_1X_1$

• 几何意义：不同截距但相同斜率的平行线

• 参数意义：$\beta_2 = E(Y|X_2=1) - E(Y|X_2=0) = E(Y|M_1) - E(Y|M_2)$

  • $\beta_2$ 表示两个水平之间平均响应的差异

交互效应（Interaction Effects）

含交互项的模型

• 模型形式：$E(Y|X) = \beta_0 + \beta_1X_1 + \beta_2X_2 + \beta_3X_1X_2$

• 模型解释：

  • 对于水平 $M_1$：$E(Y|X) = (\beta_0 + \beta_2) + (\beta_1 + \beta_3)X_1$
  • 对于水平 $M_2$：$E(Y|X) = \beta_0 + \beta_1X_1$

交互效应的意义

• 几何意义：不同截距和不同斜率的非平行线

• 参数解释：

  • $\beta_2$：两个水平在 $X_1=0$ 时的截距差异
  • $\beta_3$：两个水平的斜率差异

• 交互项：$X_1X_2$ 允许斜率随定性变量水平变化

扩展说明

多定性预测变量

• 可以包含多个定性预测变量

• 每个定性变量需要单独编码

多水平定性变量

对于有5个水平的定性变量，编码方法：

方法1：序数编码（不推荐）

• 直接编码为1, 2, 3, 4, 5

• 问题：隐含序数关系，可能不符合实际

方法2：虚拟变量编码（推荐）

• 定义4个虚拟变量 $X_1, X_2, X_3, X_4$

• $X_j = 1$ 如果水平 $j$，否则为0（$j=1,2,3,4$）

• 基准水平：第5个水平作为参考基准

方法3：效应编码

• 定义 $X_1, X_2, X_3, X_4$

• $X_j = 1$ 如果水平 $j$，$X_j = -1$ 如果水平5，否则为0

• 特点：参数表示与总体均值的偏差

定性预测变量通过虚拟变量编码引入回归模型，交互效应允许不同组别具有不同的斜率。多水平定性变量需要谨慎编码以避免虚假的序数关系，虚拟变量编码是最常用的方法。正确的编码方式对于模型解释和统计推断至关重要。