SDSC6007 课程 1

#sdsc6007

English / 中文

简介

离散时间动态系统 (The Discrete-Time Dynamic System)

该系统具有以下形式：

xk+1=fk(xk,uk,wk),k=0,1,…,N−1,x_{k + 1} = f_{k} (x_k, u_k, w_k ), \quad k = 0, 1, \ldots , N − 1,

其中：

  • kk：离散时间索引

  • NN：时间范围（Horizon）或控制被应用的次数

  • xkx_k：系统的状态，属于状态集合 SkS_k

  • uku_k：在时间 kk 需要选择的控制变量/决策变量/动作（control/decision variable/action），从集合 Uk(xk)U_k (x_k ) 中选择

  • wkw_k：一个随机参数（也称为扰动 disturbance）

  • fkf_k：描述状态如何更新的函数

假设 (Assumption)
wkw_k 是相互独立的。其概率分布可能依赖于 xkx_k 和 uku_k。

本质上是对该系统在离散的时间/控制状态内通过有限/无限状态 xNx_N 以描述整个系统，该状态在时序上受到 uk∈Uk(xk)u_k \in U_k (x_k ) 决策变量/动作与随机参数 wkw_k 影响与控制。

代价函数 (The Cost Function)

（期望）代价具有以下形式：

E[gN(xN)+∑k=0N−1gk(xk,uk,wk)]\mathbb{E} \left[ g_N (x_N ) + \sum^{N−1}_{k=0}{g_k (x_k, u_k, w_k )} \right]

其中：

  • gk(xk,uk,wk)g_k(x_k, u_k, w_k)：在时间 kk 产生的代价

  • gN(xN)g_N(x_N)：在过程结束时产生的终端代价 (terminal cost)

注意 (Note)
由于 wkw_k 的存在，代价是一个随机变量，因此我们是在优化其期望值。

没啥好说的，就是损失函数的集合形式。

确定性调度问题

示例
教授计划生产性能优于现用BearPods 3的豪华耳机，需在特定机器上执行A、B、C、D四个操作，且满足：

  1. 操作B必须在操作A完成后执行

  2. 操作D必须在操作C完成后执行

定义：

  • CmnC_{mn}：从操作 mm 切换到 nn 的准备成本

  • 初始启动成本 SAS_A 或 SCS_C（只能从A或C开始）

解法

  • 需做三次决策（最后一次由前三次决定）

  • 确定性系统（无 wkw_k）

  • 有限状态数问题 ⇒ 状态转移图

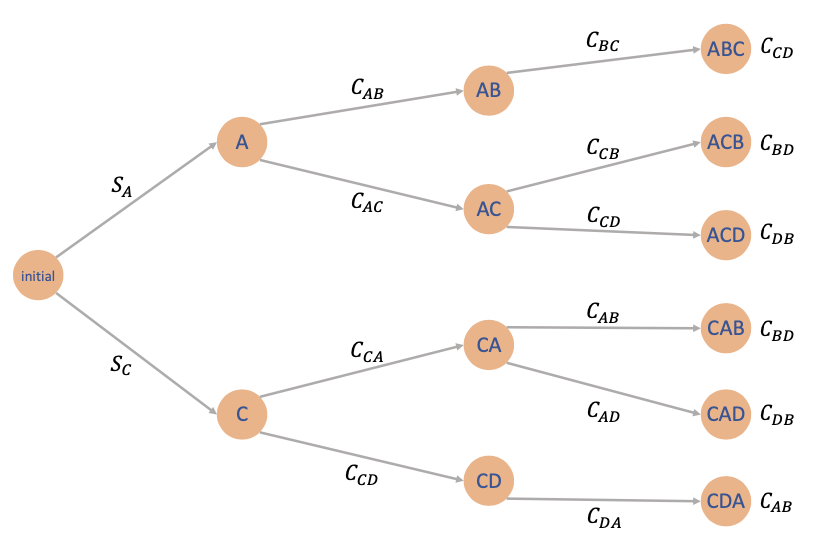
确定性调度问题状态转移图

离散状态与有限状态问题

为描述状态间转移，常定义转移概率：

pij(u,k)=P(xk+1=j∣xk=i,uk=u)p_{ij}(u,k) = \mathbb{P}(x_{k+1} = j | x_k = i, u_k = u)

在动态系统中，这等价于 xk+1=wkx_{k+1} = w_k，其中 wkw_k 服从由 pij(u,k)p_{ij}(u,k) 定义的概率分布。

示例：机器维护问题

考虑 NN 周期问题，机器可能处于 nn 种状态之一：

  • g(i)g(i)：状态 ii 下每周期的运行成本，满足 g(1)≤g(2)≤⋯≤g(n)g(1) \leq g(2) \leq \cdots \leq g(n)（状态 ii 效率高于 i+1i+1）

  • 状态转移概率：
    pij=P(下一状态为 j∣当前状态为 i)p_{ij} = \mathbb{P}(\text{下一状态为 } j \mid \text{当前状态为 } i )，且 pij=0p_{ij} = 0（若 j<ij < i）

  • 每周期初可选择：

    1. 继续运行：按转移概率演化
    2. 维修机器：支付成本 RR 使状态重置为 11（并在该周期保持状态 11）

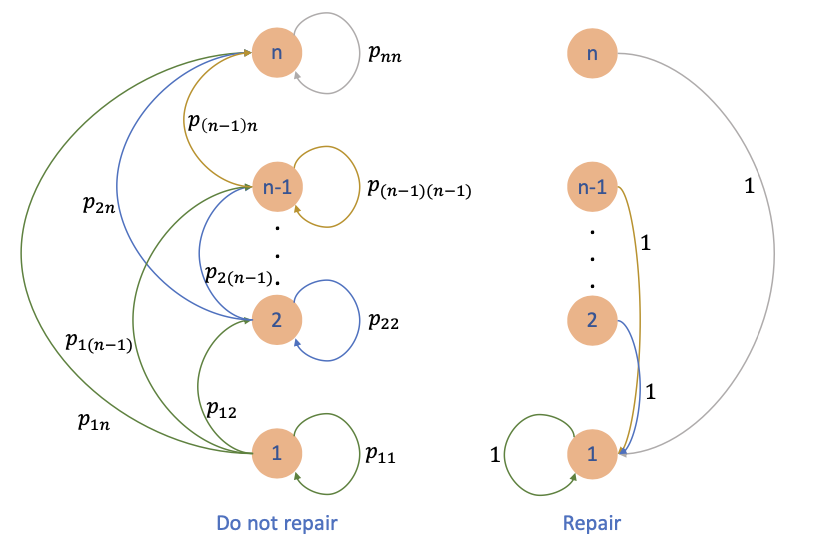
机器状态转移示意图

库存控制问题

通过每阶段订购物品满足随机需求：

  • xkx_k：第 kk 周期初可用库存

  • uku_k：第 kk 周期初订购并交付的库存量

  • wkw_k：第 kk 周期随机需求（给定概率分布）

  • r(⋅)r(\cdot)：库存过剩/缺货的惩罚成本函数

  • cc：单位订购成本

总成本函数：
gk(xk,uk,wk)=c⋅uk+r(xk+uk−wk)g_k(x_k, u_k, w_k) = c \cdot u_k + r(x_k + u_k - w_k)

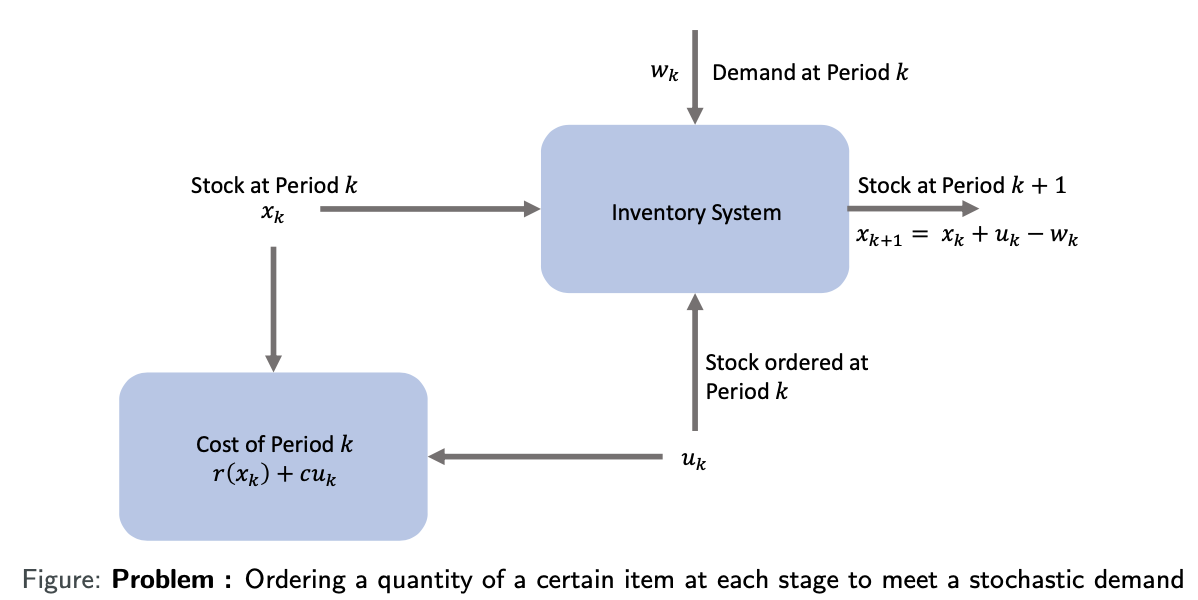
库存控制问题示意图

例子：最优解分析

假设 (u0⋆,u1⋆,…,uN−1⋆)(u_0^{\star}, u_1^\star, \ldots, u_{N-1}^\star) 是以下优化问题的最优解：

min⁡E[R(xN)+∑k=0N−1(r(xk+uk−wk)+c⋅uk)]\min \mathbb{E} \left[ R(x_N) + \sum_{k=0}^{N-1} \left( r(x_k + u_k - w_k) + c \cdot u_k \right) \right]

若需求 w1=w2=⋯=wN−1=0w_1 = w_2 = \cdots = w_{N-1} = 0 时
（即第1至第N-1周期需求恒为零）

关键结论

原随机最优解 {uk⋆}\{u_k^\star\} 非全局最优，可通过动态调整策略进一步优化成本

原因分析

  1. 信息价值未被利用
    原解基于需求随机性设计，未利用"后续需求为零"的确定性信息

  2. 库存成本可优化

  • 当已知后续无需求时，可减少早期订购量避免库存积压

  • 延迟订购决策至必要时刻，降低库存持有成本

例：原方案在周期1大量备货，但实际后续需求为零，导致不必要库存成本
3. 动态调整优势
采用状态反馈策略：

uk∗=πk(xk)u_k^* = \pi_k(x_k)

根据实时库存 xkx_k 动态调整订购量，比固定序列 {uk⋆}\{u_k^\star\} 更优

开环控制与闭环控制

开环控制 (Open-loop Control)

在初始时刻 k=0k=0，给定初始状态 x0x_0，寻找最优控制序列 (u0⋆,u1⋆,…,uN−1⋆)(u_0^\star, u_1^\star, \ldots, u_{N-1}^\star) 以最小化期望总成本：

  • 关键特性：后续状态信息不被用于调整控制决策

  • 决策方式：所有决策在初始时刻一次性确定

  • 数学表示：

    min⁡u0,…,uN−1E[∑k=0N−1gk(xk,uk,wk)+gN(xN)]\min_{u_0,\dots,u_{N-1}} \mathbb{E} \left[ \sum_{k=0}^{N-1} g_k(x_k,u_k,w_k) + g_N(x_N) \right]

闭环控制 (Closed-loop Control)

在每个时刻 kk，基于当前状态信息 xkx_k 实时做出决策（例如在时间 kk 的订购决策）：

  • 核心目标：寻找状态反馈策略 μk(⋅)\mu_k(\cdot)，将状态 xkx_k 映射为控制 uku_k

  • 决策特性：

  • 在每个决策点 kk 重新优化

  • 为每个可能状态值 xkx_k 设计控制规则

  • 计算特性：

  • 计算开销更大（需实时计算状态映射）

  • 无不确定性时性能与开环控制相同

  • 数学表示：

    uk=μk(xk)u_k = \mu_k(x_k)

闭环控制 (Closed-loop Control)

核心概念

  • 控制律定义
    设 μk(⋅)\mu_k(\cdot) 为将状态 xkx_k 映射到控制量 uku_k 的函数，即：

uk=μk(xk)u_k = \mu_k(x_k)

  • 控制策略
    定义策略 π\pi 为控制律的时序集合：

π=μ0,μ1,…,μN−1\pi = {\mu_0, \mu_1, \ldots, \mu_{N-1}}

  • 策略代价函数
    给定初始状态 x0x_0，策略 π\pi 的期望代价为：

Jπ(x0)=E[gN(xN)+∑k=0N−1gk(xk,μk(xk),wk)]J_{\pi}(x_0) = \mathbb{E} \left[ g_N (x_N) + \sum_{k=0}^{N-1} g_k \big( x_k, \mu_k(x_k), w_k \big) \right]

可行策略 (Admissible Policy)

策略 π={μ0,…,μN−1}\pi = \{\mu_0, \ldots, \mu_{N-1}\} 称为可行策略当且仅当满足：

μk(xk)∈Uk(xk),∀xk∈Sk, ∀k=0,1,…,N−1\mu_k(x_k) \in U_k(x_k), \quad \forall x_k \in S_k, \ \forall k = 0,1,\ldots,N-1

即每个时刻 kk 的每个可能状态 xkx_k，控制量 uku_k 必须属于允许控制集 Uk(xk)U_k(x_k)。

特性分析

特性 说明
实时性 控制决策基于当前状态实时生成
适应性 自动响应系统状态变化和外部扰动
计算复杂度 需为所有可能状态设计控制律，计算开销较大
最优性保证 在随机环境下优于开环控制
实现要求 需要完整的实时状态观测系统

总结

定义

考虑函数 J∗J^*，定义为：

J∗(x0)=min⁡π∈ΠJπ(x0),∀x0∈S0J^*(x_0) = \min_{\pi \in \Pi} J^{\pi}(x_0), \quad \forall x_0 \in S_0

其中：

  • Π\Pi：所有可行策略的集合

  • Jπ(x0)J^{\pi}(x_0)：策略 π\pi 从初始状态 x0x_0 开始的期望代价

称 J∗J^* 为最优值函数（optimal value function）。

关键特性

  1. 全局最优性
    J∗J^* 给出了从任意初始状态 x0x_0 出发的最小可能期望代价

  2. 策略无关性
    与具体策略无关，表示理论上的性能极限

  3. 基准作用
    任何可行策略 π\pi 都满足：

Jπ(x0)≥J∗(x0),∀x0∈S0J^{\pi}(x_0) \geq J^*(x_0), \quad \forall x_0 \in S_0

计算意义

  • 动态规划核心目标：通过逆向归纳法精确计算 J∗J^*

  • 控制工程应用：比较实际策略与理论最优值的差距

动态规划算法（DP）

最优性原理 (Principle of Optimality)

定理表述

设 π∗={μ0∗,μ1∗,…,μN−1∗}\pi^* = \{\mu_0^*, \mu_1^*, \ldots, \mu_{N-1}^*\} 是基本问题的最优策略，且在采用 π∗\pi^* 时，系统在时刻 ii 以正概率到达状态 xix_i。考虑以下子问题：

min⁡E[gN(xN)+∑k=iN−1gk(xk,μk(xk),wk)]\min \mathbb{E} \left[ g_N(x_N) + \sum_{k=i}^{N-1} g_k \big( x_k, \mu_k(x_k), w_k \big) \right]

（即从时刻 ii 状态 xix_i 开始最小化剩余代价）

则截断策略 {μi∗,μi+1∗,…,μN−1∗}\{\mu_i^*, \mu_{i+1}^*, \ldots, \mu_{N-1}^*\} 是该子问题的最优策略。

###course information# 核心内涵

  • 分段构造：最优策略可通过分段方式构造

  • 尾部优先：首先求解尾部子问题（从最终阶段开始）

  • 逆向扩展：逐步向前扩展至原始问题

  1. 最优策略的遗传性
    全局最优策略的任意后续片段，对其起始状态而言也是最优的

  2. 时间一致性
    最优决策不仅考虑当前代价，还考虑后续状态的最优演化路径

  3. 逆向求解基础
    该原理保证了动态规划逆向归纳法的有效性

动态规划算法 - 库存控制示例

例子
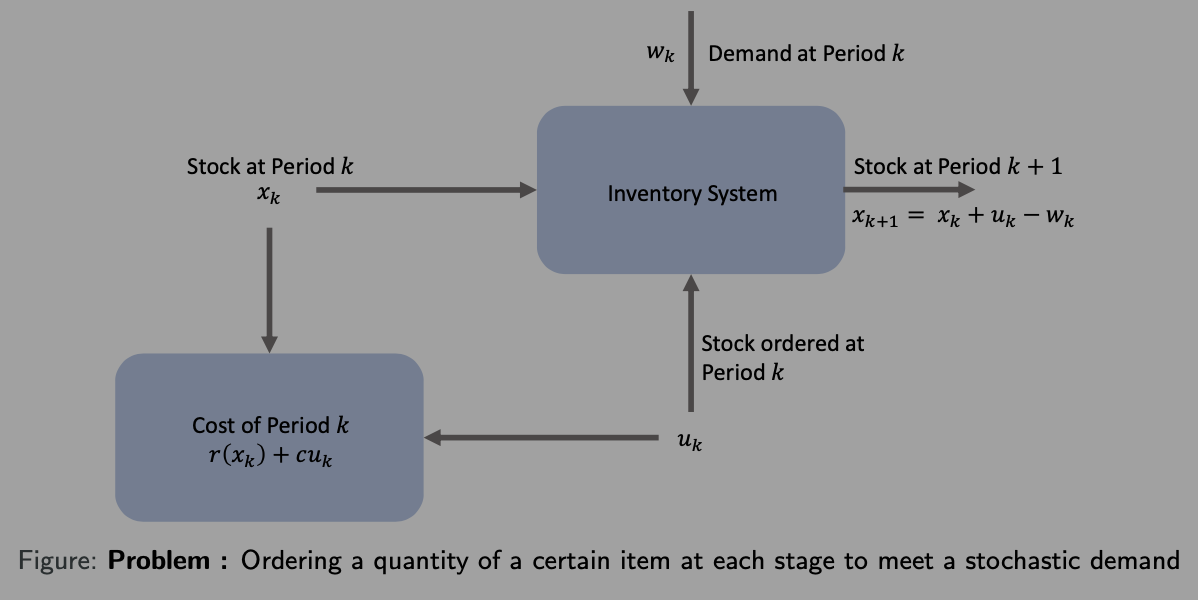
Inventory Control Example.png

尾部子问题求解流程

核心思想：逆向求解，从最终阶段逐步向前递推

  1. 长度1的尾部问题（时刻 k=N−1k = N-1）

    • 决策目标：最小化当期成本与终端成本期望值

      minimizec⋅uN−1+EwN−1[R(xN)]\text{minimize} \quad c \cdot u_{N-1} + \mathbb{E}_{w_{N-1}} \left[ R(x_N) \right]

      • c⋅uN−1c \cdot u_{N-1}：当期订购成本
      • EwN−1[R(xN)]\mathbb{E}_{w_{N-1}} \left[ R(x_N) \right]：终端库存成本的期望值

    • 状态转移关系：xN=xN−1+uN−1−wN−1x_N = x_{N-1} + u_{N-1} - w_{N-1}

      ⇒minimizec⋅uN−1+EwN−1[R(xN−1+uN−1−wN−1)]\Rightarrow \text{minimize} \quad c \cdot u_{N-1} + \mathbb{E}_{w_{N-1}} \left[ R(x_{N-1} + u_{N-1} - w_{N-1}) \right]

    • 值函数计算：

      JN−1(xN−1)=r(xN−1)+min⁡uN−1≥0{c⋅uN−1+EwN−1[R(xN−1+uN−1−wN−1)]}J_{N-1}(x_{N-1}) = r(x_{N-1}) + \min_{u_{N-1} \geq 0} \left\{ c \cdot u_{N-1} + \mathbb{E}_{w_{N-1}} \left[ R(x_{N-1} + u_{N-1} - w_{N-1}) \right] \right\}

      • r(xN−1)r(x_{N-1})：当期库存持有/缺货成本
      • 需为所有 xN−1∈SN−1x_{N-1} \in S_{N-1} 计算该值函数

  2. 长度2的尾部问题（时刻 k=N−2k = N-2）

    • 决策目标：最小化当期成本与后续成本期望值

      minimizer(xN−2)+c⋅uN−2+EwN−2[JN−1(xN−1)]\text{minimize} \quad r(x_{N-2}) + c \cdot u_{N-2} + \mathbb{E}_{w_{N-2}} \left[ J_{N-1}(x_{N-1}) \right]

    • 状态转移关系：xN−1=xN−2+uN−2−wN−2x_{N-1} = x_{N-2} + u_{N-2} - w_{N-2}

      ⇒minimizer(xN−2)+c⋅uN−2+EwN−2[JN−1(xN−2+uN−2−wN−2)]\Rightarrow \text{minimize} \quad r(x_{N-2}) + c \cdot u_{N-2} + \mathbb{E}_{w_{N-2}} \left[ J_{N-1}(x_{N-2} + u_{N-2} - w_{N-2}) \right]

    • 值函数计算：

      JN−2(xN−2)=r(xN−2)+min⁡uN−2≥0{c⋅uN−2+EwN−2[JN−1(xN−2+uN−2−wN−2)]}J_{N-2}(x_{N-2}) = r(x_{N-2}) + \min_{u_{N-2} \geq 0} \left\{ c \cdot u_{N-2} + \mathbb{E}_{w_{N-2}} \left[ J_{N-1}(x_{N-2} + u_{N-2} - w_{N-2}) \right] \right\}

  3. 通用递推公式（长度 N−kN-k 的尾部问题）

    Jk(xk)=r(xk)+min⁡uk≥0{c⋅uk+Ewk[Jk+1(xk+uk−wk)]}J_k(x_k) = r(x_k) + \min_{u_k \geq 0} \left\{ c \cdot u_k + \mathbb{E}_{w_k} \left[ J_{k+1}(x_k + u_k - w_k) \right] \right\}

    • r(xk)r(x_k)：kk 时刻库存成本
    • c⋅ukc \cdot u_k：kk 时刻订购成本
    • Ewk[Jk+1(⋅)]\mathbb{E}_{w_k} \left[ J_{k+1}(\cdot) \right]：后续最优成本的期望

最终目标：通过 k=0k=0 时的尾部问题（长度 NN）获得原问题最优解

动态规划算法 (The DP Algorithm)

对于任意初始状态 x0x_0，基本问题的最优成本 J∗(x0)J^*(x_0) 等于 J0(x0)J_0(x_0)，由以下逆向算法（从 N−1N-1 到 00）给出：

边界条件：

JN(xN)=gN(xN)J_N(x_N) = g_N(x_N)

递推关系：

Jk(xk)=min⁡uk∈Uk(xk)Ewk[gk(xk,uk,wk)+Jk+1(fk(xk,uk,wk))](⋆)J_k(x_k) = \min_{u_k \in U_k(x_k)} \mathbb{E}_{w_k} \left[ g_k(x_k,u_k,w_k) + J_{k+1}\big(f_k(x_k,u_k,w_k)\big) \right] \quad (\star)

其中期望 Ewk\mathbb{E}_{w_k} 针对 wkw_k 的概率分布（依赖于 xkx_k 和 uku_k）。若 uk⋆=μk⋆(xk)u_k^\star = \mu_k^\star(x_k) 使 (⋆)(\star) 式右端最小化，则策略 π⋆={μ0⋆,…,μN−1⋆}\pi^\star = \{\mu_0^\star, \ldots, \mu_{N-1}^\star\} 是最优的。

关键定义

  • Jk(xk)J_k(x_k)：在状态 xkx_k 和时间 kk 的剩余成本（cost-to-go）

  • JkJ_k：时间 kk 的剩余成本函数

算法证明（非正式）

基本设定

  1. 定义子策略 πk={μk,μk+1,…,μN−1}\pi_k = \{\mu_k, \mu_{k+1}, \ldots, \mu_{N-1}\}

  2. 设 Jk⋆(xk)J_k^\star(x_k) 为从 (xk,k)(x_k, k) 开始的 (N−k)(N-k) 阶段最优成本：

Jk⋆(xk)=min⁡πkEwk,…,wN−1[gN(xN)+∑i=kN−1gi(xi,μi(xi),wi)]J_k^\star(x_k) = \min_{\pi_k} \mathbb{E}_{w_k,\ldots,w_{N-1}} \left[ g_N(x_N) + \sum_{i=k}^{N-1} g_i\big(x_i, \mu_i(x_i), w_i\big) \right]

  1. 边界条件：

    • k=0k=0 时：J0⋆J_0^\star 是原问题最优值函数
    • k=Nk=N 时：JN⋆=gN(xN)J_N^\star = g_N(x_N)
归纳证明

目标：证明 Jk⋆=JkJ_k^\star = J_k（DP算法值）

  1. 归纳基础：k=Nk=N 时成立（JN⋆=gN(xN)=JNJ_N^\star = g_N(x_N) = J_N）

  2. 归纳假设：假设 ∀xk+1∈Sk+1\forall x_{k+1} \in S_{k+1}，有 Jk+1⋆(xk+1)=Jk+1(xk+1)J_{k+1}^\star(x_{k+1}) = J_{k+1}(x_{k+1})

  3. 推导过程：

Jk⋆(xk)=min⁡(μk,πk+1)Ewk,…,wN−1[gN(xN)+∑i=kN−1gi(xi,μi(xi),wi)]=min⁡(μk,πk+1)E[gk(xk,μk(xk),wk)+gN(xN)+∑i=k+1N−1gi(⋯ )]=min⁡μkEwk[gk(xk,μk(xk),wk)+min⁡πk+1Ewk+1,…,wN−1[gN(xN)+∑i=k+1N−1gi(⋯ )]]（最优性原理）=min⁡μkEwk[gk(xk,μk(xk),wk)+Jk+1⋆(fk(xk,μk(xk),wk))]=min⁡μkEwk[gk(xk,μk(xk),wk)+Jk+1(fk(xk,μk(xk),wk))]（由归纳假设）=min⁡ukEwk[gk(xk,uk,wk)+Jk+1(fk(xk,uk,wk))]=Jk(xk) \begin{align*} J_k^\star(x_k) &= \min_{(\mu_k, \pi_{k+1})} \mathbb{E}_{w_k,\ldots,w_{N-1}} \left[ g_N(x_N) + \sum_{i=k}^{N-1} g_i\big(x_i, \mu_i(x_i), w_i\big) \right] \\ &= \min_{(\mu_k, \pi_{k+1})} \mathbb{E} \left[ g_k(x_k, \mu_k(x_k), w_k) + g_N(x_N) + \sum_{i=k+1}^{N-1} g_i(\cdots) \right] \\ &= \min_{\mu_k} \mathbb{E}_{w_k} \left[ g_k(x_k, \mu_k(x_k), w_k) + \min_{\pi_{k+1}} \mathbb{E}_{w_{k+1},\ldots,w_{N-1}} \left[ g_N(x_N) + \sum_{i=k+1}^{N-1} g_i(\cdots) \right] \right] \\ &\quad \text{（最优性原理）} \\ &= \min_{\mu_k} \mathbb{E}_{w_k} \left[ g_k(x_k, \mu_k(x_k), w_k) + J_{k+1}^\star\big(f_k(x_k, \mu_k(x_k), w_k)\big) \right] \\ &= \min_{\mu_k} \mathbb{E}_{w_k} \left[ g_k(x_k, \mu_k(x_k), w_k) + J_{k+1}\big(f_k(x_k, \mu_k(x_k), w_k)\big) \right] \\ &\quad \text{（由归纳假设）} \\ &= \min_{u_k} \mathbb{E}_{w_k} \left[ g_k(x_k, u_k, w_k) + J_{k+1}\big(f_k(x_k, u_k, w_k)\big) \right] \\ &= J_k(x_k) \end{align*}

动态规划算法 - 烘焙示例

问题描述

博士需用两个烤箱烘焙蛋糕，系统动态和成本函数如下：

  • 状态方程：xk+1=(1−a)⋅xk+a⋅uk,k=0,1x_{k+1} = (1-a) \cdot x_k + a \cdot u_k, \quad k=0,1

  • 成本函数：r⋅(x2−T)2+u02+u12r \cdot (x_2 - T)^2 + u_0^2 + u_1^2

  • 参数说明：

    • xkx_k：蛋糕在第 kk 个烤箱出口的温度
    • uku_k：第 kk 个烤箱的设定温度
    • a∈(0,1)a \in (0,1)：热传导系数
    • TT：目标温度
    • r>0r > 0：终端温度偏差的惩罚系数

动态规划求解过程

  1. 终端时刻 (k=2k=2)

J2(x2)=r⋅(x2−T)2J_2(x_2) = r \cdot (x_2 - T)^2

  1. 时刻 k=1k=1

J1(x1)=min⁡u1[u12+J2(x2)]=min⁡u1[u12+r⋅((1−a)x1+au1−T)2]\begin{align*} J_1(x_1) &= \min_{u_1} \left[ u_1^2 + J_2(x_2) \right] \\ &= \min_{u_1} \left[ u_1^2 + r \cdot \big((1-a)x_1 + a u_1 - T\big)^2 \right] \end{align*}

优化求解：

  • 对 u1u_1 求导并令导数为零：

    0=2u1+2ra((1−a)x1+au1−T)0 = 2u_1 + 2ra \big((1-a)x_1 + a u_1 - T\big)

  • 解得最优控制：

    u1∗=ra(T−(1−a)x1)1+ra2u_1^* = \frac{ra \big(T - (1-a)x_1\big)}{1 + ra^2}

  • 代入得值函数：

    J1(x1)=r((1−a)x1−T)21+ra2J_1(x_1) = \frac{r \big((1-a)x_1 - T\big)^2}{1 + ra^2}

  1. 初始时刻 (k=0k=0)

J0(x0)=min⁡u0[u02+J1(x1)]=min⁡u0[u02+r((1−a)2x0+(1−a)au0−T)21+ra2]\begin{align*} J_0(x_0) &= \min_{u_0} \left[ u_0^2 + J_1(x_1) \right] \\ &= \min_{u_0} \left[ u_0^2 + \frac{r \big((1-a)^2 x_0 + (1-a)a u_0 - T\big)^2}{1 + ra^2} \right] \end{align*}

优化求解：

  • 类似求导过程得最优控制：

    u0∗=r(1−a)a(T−(1−a)2x0)1+ra2(1+(1−a)2)u_0^* = \frac{r(1-a)a \big(T - (1-a)^2 x_0\big)}{1 + ra^2 \big(1 + (1-a)^2\big)}

  • 值函数：

    J0(x0)=r((1−a)2x0−T)21+ra2(1+(1−a)2)J_0(x_0) = \frac{r \big((1-a)^2 x_0 - T\big)^2}{1 + ra^2 \big(1 + (1-a)^2\big)}

关键结论：
此线性二次型问题可获得解析解，但大多数动态规划问题需数值求解

动态规划算法 - 库存控制示例

问题设定

  • 需求处理：未满足需求直接丢失

  • 状态转移：xk+1=max⁡{0,xk+uk−wk}x_{k+1} = \max\{0, x_k + u_k - w_k\}

  • 控制约束：xk+uk≤2x_k + u_k \leq 2

  • 成本结构：

    • 订购成本：uku_k（每单位成本为1）
    • 持有成本：(xk+uk−wk)2(x_k + u_k - w_k)^2
    • 终端成本：gN(xN)=0g_N(x_N) = 0

  • 需求分布：
    P(wk=0)=0.1, P(wk=1)=0.7, P(wk=2)=0.2\mathbb{P}(w_k=0)=0.1,\ \mathbb{P}(w_k=1)=0.7,\ \mathbb{P}(w_k=2)=0.2

  • 初始状态：x0=0, N=3x_0=0,\ N=3

逆向求解过程

需要注意，由于此时 uku_k 为随机分布，因此计算得到的 JkJ_k 为数学期望。

  1. 终端时刻 (k=3k=3)

J3(x3)=gN(xN)=0(∀x3)J_3(x_3) = g_N(x_N) = 0 \quad (\forall x_3)

  1. 时刻 k=2k=2（倒数第一阶段）

状态空间：x2∈{0,1,2}x_2 \in \{0,1,2\}

  • x2=0x_2=0：

    J2(0)=min⁡u2∈{0,1,2}Ew2[u2+(0+u2−w2)2]=min⁡{u2=0:0+0.1(0)2+0.7(−1)2+0.2(−2)2=1.5u2=1:1+0.1(1)2+0.7(0)2+0.2(−1)2=1.3u2=2:2+0.1(4)+0.7(1)+0.2(0)=3.1=1.3(u2∗=1)\begin{align*} J_2(0) &= \min_{u_2 \in \{0,1,2\}} \mathbb{E}_{w_2} \left[ u_2 + (0 + u_2 - w_2)^2 \right] \\ &= \min \begin{cases} u_2=0: & 0 + 0.1(0)^2 + 0.7(-1)^2 + 0.2(-2)^2 = 1.5 \\ u_2=1: & 1 + 0.1(1)^2 + 0.7(0)^2 + 0.2(-1)^2 = 1.3 \\ u_2=2: & 2 + 0.1(4) + 0.7(1) + 0.2(0) = 3.1 \end{cases} \\ &= 1.3 \quad (u_2^*=1) \end{align*}

  • x2=1x_2=1：

    J2(1)=min⁡u2∈{0,1}Ew2[u2+(1+u2−w2)2]=min⁡{u2=0:0+0.1(1)2+0.7(0)2+0.2(−1)2=0.3u2=1:1+0.1(4)+0.7(1)+0.2(0)=2.1=0.3(u2∗=0)\begin{align*} J_2(1) &= \min_{u_2 \in \{0,1\}} \mathbb{E}_{w_2} \left[ u_2 + (1 + u_2 - w_2)^2 \right] \\ &= \min \begin{cases} u_2=0: & 0 + 0.1(1)^2 + 0.7(0)^2 + 0.2(-1)^2 = 0.3 \\ u_2=1: & 1 + 0.1(4) + 0.7(1) + 0.2(0) = 2.1 \end{cases} \\ &= 0.3 \quad (u_2^*=0) \end{align*}

  • x2=2x_2=2：

    J2(2)=min⁡u2∈{0}Ew2[u2+(2+u2−w2)2]=0+0.1(4)+0.7(1)+0.2(0)=1.1(u2∗=0)\begin{align*} J_2(2) &= \min_{u_2 \in \{0\}} \mathbb{E}_{w_2} \left[ u_2 + (2 + u_2 - w_2)^2 \right] \\ &= 0 + 0.1(4) + 0.7(1) + 0.2(0) = 1.1 \quad (u_2^*=0) \end{align*}

值函数总结：

x2x_2 J2(x2)J_2(x_2) μ2∗(x2)\mu_2^*(x_2)
0 1.3 1
1 0.3 0
2 1.1 0

  1. 继续求解 (k=1,0k=1,0)

类似方法计算 J1(x1)J_1(x_1) 和 J0(x0)J_0(x_0)，需考虑状态转移：

xk+1=max⁡{0,xk+uk−wk}x_{k+1} = \max\{0, x_k + u_k - w_k\}

计算复杂度分析

  • 状态空间：∣Sk∣=3|S_k| = 3（本例）

  • 控制空间：∣Uk∣≤3|U_k| \leq 3（本例）

  • 时间复杂度：O(N⋅∣S∣⋅∣U∣⋅∣W∣)O(N \cdot |S| \cdot |U| \cdot |W|)

  • 实际挑战：状态空间随维度指数增长（维度灾难）

动态规划算法 - 有限状态系统

系统描述

考虑具有以下特性的有限状态系统：

  • 状态转移概率：pij(u)=P(xk+1=j∣xk=i,uk=u)p_{ij}(u) = \mathbb{P}(x_{k+1} = j \mid x_k = i, u_k = u)

  • 动态方程：xk+1=wkx_{k+1} = w_k，其中 wkw_k 服从由 pij(u)p_{ij}(u) 定义的概率分布

关键假设

  1. 平稳性：

    • 转移概率 pij(u)p_{ij}(u) 与时间 kk 无关
    • 控制约束集 Uk(i)=U(i)U_k(i) = U(i) 恒定

  2. 成本特性：

    • 阶段成本 g(i,u)g(i,u) 独立于随机扰动 wkw_k

动态规划算法

递推公式：

Jk(i)=min⁡u∈U(i)[g(i,u)+E[Jk+1(wk)]]J_k(i) = \min_{u \in U(i)} \left[ g(i,u) + \mathbb{E} \left[ J_{k+1}(w_k) \right] \right]

显式形式：

Jk(i)=min⁡u∈U(i)[g(i,u)+∑jpij(u)Jk+1(j)]J_k(i) = \min_{u \in U(i)} \left[ g(i,u) + \sum_{j} p_{ij}(u) J_{k+1}(j) \right]

计算特性

特性 说明
状态空间 有限（i∈{1,2,…,n}i \in \{1,2,\dots,n\}）
控制空间 有限（u∈U(i)u \in U(i)）
复杂度 $O(N \cdot n^2 \cdot
优势 避免连续状态空间的维度灾难

应用场景：马尔可夫决策过程（MDP）、排队系统、网络路由等离散状态问题

状态增强与系统重构技术

1. 时间滞后处理

问题：当状态转移依赖历史状态（如 xk+1=fk(xk,xk−1,uk,uk−1,wk)x_{k+1} = f_k(x_k, x_{k-1}, u_k, u_{k-1}, w_k)）

解决方案：状态增强
定义新状态向量：

x~k=[xkyksk]=[xkxk−1uk−1]\tilde{x}_k = \begin{bmatrix} x_k \\ y_k \\ s_k \end{bmatrix} = \begin{bmatrix} x_k \\ x_{k-1} \\ u_{k-1} \end{bmatrix}

新状态转移方程：

x~k+1=[xk+1yk+1sk+1]=[fk(xk,yk,uk,sk,wk)xkuk]=f~k(x~k,uk,wk)\tilde{x}_{k+1} = \begin{bmatrix} x_{k+1} \\ y_{k+1} \\ s_{k+1} \end{bmatrix} = \begin{bmatrix} f_k(x_k, y_k, u_k, s_k, w_k) \\ x_k \\ u_k \end{bmatrix} = \tilde{f}_k(\tilde{x}_k, u_k, w_k)

关键点：将历史状态 xk−1x_{k-1} 和历史控制 uk−1u_{k-1} 作为当前状态的一部分

2. 相关干扰处理

问题：扰动项相关（如 wk=λwk−1+ξkw_k = \lambda w_{k-1} + \xi_k）

解决方案：状态增强
定义新状态向量：

x~k=[xkyk]其中yk=wk−1\tilde{x}_k = \begin{bmatrix} x_k \\ y_k \end{bmatrix} \quad \text{其中} \quad y_k = w_{k-1}

新状态转移方程：

x~k+1=[xk+1yk+1]=[fk(xk,uk,λyk+ξk)λyk+ξk]=f~k(x~k,uk,ξk)\tilde{x}_{k+1} = \begin{bmatrix} x_{k+1} \\ y_{k+1} \end{bmatrix} = \begin{bmatrix} f_k(x_k, u_k, \lambda y_k + \xi_k) \\ \lambda y_k + \xi_k \end{bmatrix} = \tilde{f}_k(\tilde{x}_k, u_k, \xi_k)

推广形式：对 wk=Ckyk+1w_k = C_k y_{k+1}, yk+1=Akyk+ξky_{k+1} = A_k y_k + \xi_k：

x~k+1=[fk(xk,uk,Ck(Akyk+ξk))Akyk+ξk]\tilde{x}_{k+1} = \begin{bmatrix} f_k(x_k, u_k, C_k(A_k y_k + \xi_k)) \\ A_k y_k + \xi_k \end{bmatrix}

3. 预测信息整合

问题：决策前已知扰动分布信息（如天气预报影响需求分布）

建模：

  • wk∼Qiw_k \sim Q_i (i∈{1,…,m}i \in \{1,\dots,m\})

  • ii 在决策 uku_k 前已知

  • 预测过程：yk+1=ξky_{k+1} = \xi_k (ξk\xi_k 独立，P(ξk=i)=piP(\xi_k=i)=p_i)

增强状态：

x~k=[xkyk]\tilde{x}_k = \begin{bmatrix} x_k \\ y_k \end{bmatrix}

其中 yky_k 存储下一时刻扰动分布信息

状态转移：

x~k+1=[xk+1yk+1]=[fk(xk,uk,wk)ξk]\tilde{x}_{k+1} = \begin{bmatrix} x_{k+1} \\ y_{k+1} \end{bmatrix} = \begin{bmatrix} f_k(x_k, u_k, w_k) \\ \xi_k \end{bmatrix}

决策优势：uku_k 可基于 yky_k（未来扰动分布）优化决策