确定性系统与最短路问题
#sdsc6007
English / 中文
简介
最短路径问题 (Shortest Path Problems)
问题定义
给定节点集合 {1,2,…,N,t}(t 为目标节点),
-
aij:从节点 i 到 j 的路径成本(aij=∞ 表示无直接路径)
-
关键假设:所有环路成本非负(∀循环路径 i→j1→⋯→jk→i, 总成本≥0)
-
目标:寻找从任意节点 i 到 t 的最小成本路径
非负环路假设的重要性
核心意义:确保最优解存在且路径长度有限
-
避免无限负成本:
若存在负成本循环 cycle∑aij<0⇒总成本可无限降低
例:反复经过负成本环路使总成本趋于 −∞
-
自环约束:
aii≥0(若允许节点停留)
-
路径长度界限:
最优路径最多包含 N 次移动
- 可通过设置 aii=0 强制路径恰好有 N 次移动(允许停留)
动态规划建模
定义值函数:
Jk(i)=从 i 出发经 k 步到 t 的最小成本
递推方程:
Jk(i)=jmin[aij+Jk−1(j)]
边界条件:
J0(t)=0,J0(i)=∞ (i=t)
非负环路假设的实际意义:
该假设保证了最短路径问题具有良好定义的最优解。若存在负成本环路,则算法可能陷入无限循环,无法收敛。
在路由选择、网络优化等实际应用中,该条件通常通过成本函数设计自然满足(如距离、时延等物理量非负)。
确定性动态规划问题
确定性系统特性
核心特征:无随机扰动 (wk 不存在或为已知常量)
-
状态转移完全可预测:
xk+1=fk(xk,uk)
- 给定初始状态 x0 和策略 {μ0,…,μN−1},可精确计算状态轨迹
-
闭环控制无优势:
Jclosed-loop=Jopen-loop
- 最优开环控制序列 (u0∗,u1∗,…,uN−1∗) 与闭环策略 μk∗(xk) 成本相同
为什么闭环控制无优势:
在确定性系统中,未来状态完全由当前决策决定。一旦选定决策序列,状态轨迹即确定。实时状态反馈不提供新信息,因此闭环策略无法改进开环策略的成本。
有限状态系统建模
状态转移图表示:
-
节点:状态 xk∈Sk(有限集合)
-
有向边:控制决策 uk 驱动的状态转移
xkukxk+1=fk(xk,uk)
-
边成本:阶段成本 gk(xk,uk)
关键简化:对每个状态转移 xk→xk+1,仅需保留最小成本决策:
ck(xk,xk+1)=uk∈Uk(xk)fk(xk,uk)=xk+1mingk(xk,uk)
动态规划方程
值函数递推:
Jk(xk)=xk+1min[ck(xk,xk+1)+Jk+1(xk+1)]
边界条件:
JN(xN)=gN(xN)
计算意义:将原问题转化为多阶段图的最短路径问题
有限状态系统的本质:
通过状态转移图建模后,问题退化为寻找从初始状态到终端状态的最小成本路径。动态规划在此场景下本质是逆向搜索图的最优路径。
确定性有限状态系统与最短路径问题的等价关系
确定性系统 → 最短路径问题 (SPP)
转换方法:
-
定义节点:
- s:初始状态节点(对应 x0)
- t:终端节点(人工添加)
-
边成本定义:
- 阶段 k 转移成本:aijk=minukgk(i,uk)(当 fk(i,uk)=j)
- i:当前状态
- j:下一状态
- uk:控制决策
- gk:阶段成本函数
- 终端成本:aitN=gN(i)
-
路径成本:
总成本=k=0∑N−1axkxk+1k+axNtN
核心等价:原问题最优成本 =J0(s)= 从 s 到 t 的最短路径长度
逆向动态规划算法
值函数定义:
Jk(i)=从状态 i 在阶段 k 到终端 t 的最小成本
递推方程:
JN(i)Jk(i)=aitN∀i∈SN(终端成本:状态 i 到 t 的直接成本)=j∈Sk+1min[aijk+Jk+1(j)]k=N−1,…,0(最小化:转移成本 aijk + 后续最优成本 Jk+1(j))
最优解:J0(s) 为最短路径长度(初始状态 s 到终端 t 的最小成本)
最短路径问题 → 确定性系统
转换方法:
-
固定阶段数 N(由非负环路假设保证)
-
定义值函数:
Jk(i)=从 i 经 N−k 步到 t 的最小成本
-
递推关系:
JN−1(i)Jk(i)=ait(一步转移成本)=j=1,…,Nmin[aij+Jk+1(j)]k=0,…,N−2(最小化:当前转移成本 aij + 后续最优成本 Jk+1(j))
关键点:J0(i) 给出从 i 到 t 的最短路径成本
前向动态规划算法(特殊性质)
仅适用于确定性SPP问题:
-
值函数定义:
J~k(j)=从 s 到 j(阶段 k)的最小成本
-
递推方程:
J~1(j)J~k(j)J~0(t)=asj0∀j∈S1(初始状态 s 到阶段1状态 j 的成本)=i∈Sk−1min[aijN−k+1+J~k−1(i)]k=2,…,N(最小化:转移成本 aijN−k+1 + 前序最优成本 J~k−1(i))=i∈SNmin[aitN+J~N(i)](终端成本:状态 i 到 t + 到达 i 的最优成本)
对比说明:
逆向DP计算"剩余成本"(cost-to-go),前向DP计算"到达成本"(cost-to-arrive)。
因路径对称性,两者在确定性SPP中等价,但前向方法不适用于随机问题。
最短路径应用:关键路径分析
问题描述
应用场景:项目管理中活动调度优化
核心目标:
-
确定项目最短完成时间
-
识别关键活动(延迟会导致项目整体延迟的活动)
案例研究:杨博士的日程优化
活动分解:
| 活动 |
描述 |
| 与助教会面 |
必须完成 |
| 回复邮件 |
|
| 午餐 |
|
| 与博士生会面 |
|
| 硕士项目工作 |
|
| 教学 |
|
阶段划分:
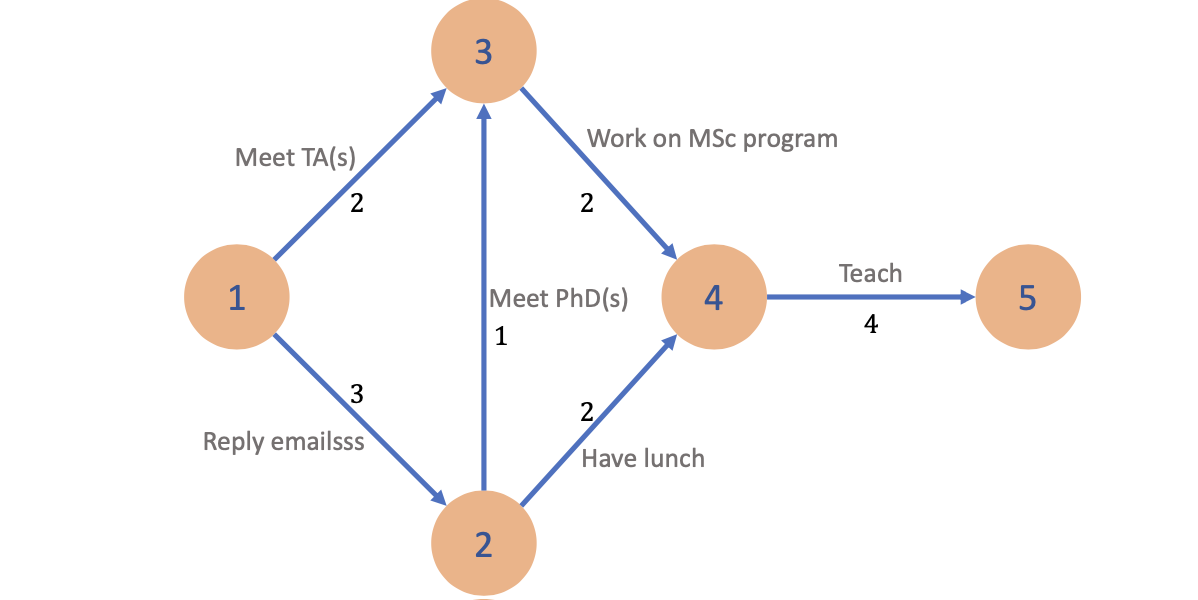
关键路径算法
| 变量 |
符号表示 |
定义说明 |
| 路径持续时间 |
Dp |
路径 p 的总持续时间
计算:Dp=∑(i,j)∈ptij |
| 最早完成时间 |
Ti |
节点 i 的最早完成时间
计算:Ti=max所有路径 p 从 1 到 iDp |
| 活动持续时间 |
tji |
活动 (j,i) 的持续时间
(从节点 j 到 i 的边权重) |
| 前驱节点集合 |
Pred(i) |
节点 i 的直接前驱节点集合
(有边直接指向 i 的节点) |
| 关键活动判定 |
Ti=Tj+tji |
活动 (j,i) 为关键活动的充要条件
(满足此等式时活动无时差) |
| 时差(松弛时间) |
Slackji |
非关键活动的可延迟时间
计算:Slackji=Ti−(Tj+tji) |
路径持续时间计算:
Dp=(i,j)∈p∑tij(路径 p 的总持续时间)
阶段最早完成时间:
Ti=所有从1到i的路径pmaxDp(节点 i 的最早完成时间)
关键路径定义:
关键路径=argpmaxDp(从节点1到节点5的最长路径)
动态规划求解
值函数定义:
Ti=节点 i 的最早完成时间
递推方程:
Ti=j∈Pred(i)max(Tj+tji)
其中 Pred(i) 是节点 i 的直接前驱集合
边界条件:
T1=0
关键活动识别:活动 (j,i) 是关键活动当且仅当:
Ti=Tj+tji
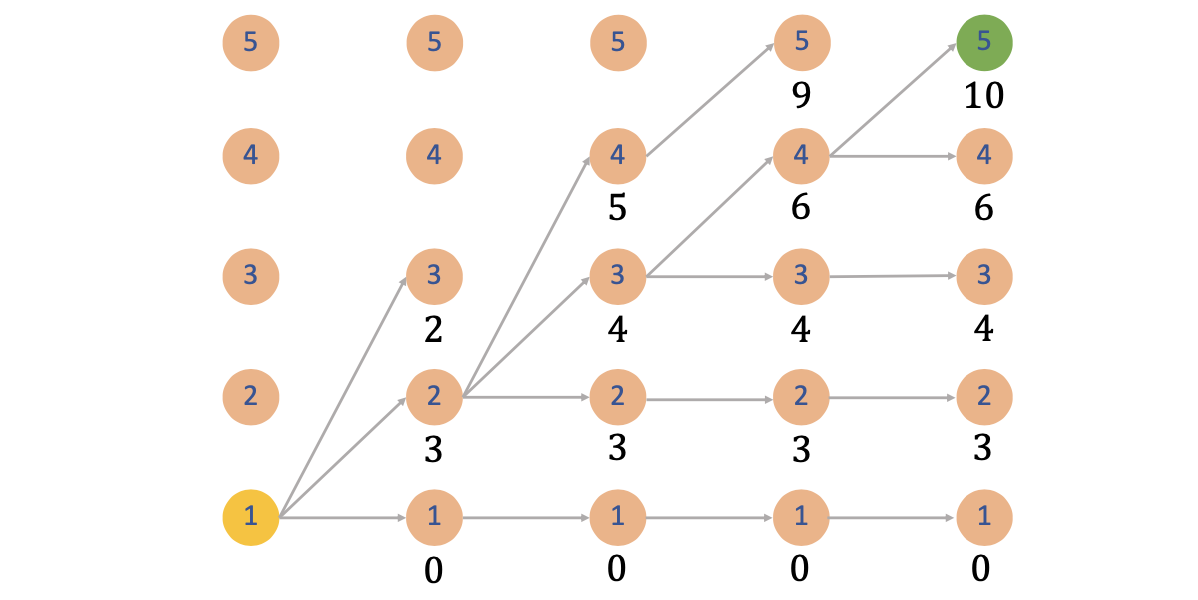
算法特性
-
无环图保证:
- 项目网络无循环 → 有限路径数
- 确保 max 运算有定义
-
关键活动特性:
管理启示:
优化关键活动可缩短总工期,非关键活动可灵活调度资源


