SDSC6012 课程 1-简介

#sdsc6012

English/ 中文

时间序列定义

核心概念

• 时间序列是按时间顺序索引的数据点序列。

• 应用领域：

  • 经济学：每日股价、GDP、月度失业率
  • 社会科学：人口、出生率、入学率
  • 流行病学：流感病例数、死亡率
  • 医学：血压监测、fMRI数据
  • 自然科学：全球温度、月度太阳黑子观测

补充说明：时间序列是现实世界动态过程的观测记录，核心特征是数据点按时间戳排序。

时间序列分析目标

分析意义

1. 描述与解释：理解序列生成机制（如趋势/季节性）

   例：分析气温序列中的长期变暖趋势

2. 预测：预测未来值

   例：预测下季度失业率

3. 控制：评估干预措施影响

   例：货币政策对失业率的影响

4. 假设检验：验证理论模型

   例：检验全球变暖假设

时间序列模型

基本分解模型

$$x_t = m_t + s_t + e_t$$

公式解释：

• $x_t$：时间 $t$ 的观测值
• $m_t$：趋势项（长期变化趋势）
• $s_t$：季节项（周期性变化规则）
• $e_t$：残差项（随机波动/噪声）

随机过程视角

• 时间序列是随机过程 $\{x_t\}$ 的一次实现（realization）

  补充说明：

  • 随机过程 = 生成序列的"自然法则"（理论模型）
  • 时间序列 = 实际观测到的具体数据（现实记录）
  • 例：每日3PM温度记录是时间序列；温度变化规律是随机过程

白噪声 (White Noise)

严格定义

白噪声是满足三条件的随机过程 $w_t$：

1. 零均值：$E(w_t) = 0$

2. 恒定方差：$\text{Var}(w_t) = \sigma_w^2$

3. 无自相关：$\text{Corr}(w_t, w_{t+k}) = 0 \ (k \neq 0)$

数学表示

$$w_t \sim \text{wn}(0, \sigma_w^2)$$

关键性质：

• 无任何可挖掘模式（完全随机）
• 过去值不影响未来值（无记忆性）

高斯白噪声

• 特殊形式：$w_t$ 服从正态分布

• 累积分布函数：

$$P(w_t < c_t) = \Phi(c_t) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{c_t} e^{-w^2/2} dw$$

平稳与非平稳时间序列

核心定义

• 平稳时间序列：其统计特性（如均值、方差）不随时间变化，序列行为与时间无关。

• 非平稳时间序列：其统计特性随时间变化，序列行为强烈依赖时间。

补充说明：平稳序列的稳定统计特性使历史模式可用于未来预测（如"前一值高则下一值回落"的规律未来仍适用）。

问题与优势

• 非平稳序列问题：统计特性持续变化，过去模式未来可能完全失效（如均值今日100明日110）。

• 平稳序列优势：固定均值和方差使行为模式一致，可靠预测成为可能。

示例：冰淇淋销售（非平稳性）

数据特征

• 夏季（7-8月）销量高峰，冬季（12-1月）销量低谷，形成重复的峰谷模式。

• 因销量与时间强相关，故为非平稳序列。

平稳化方法：季节性差分

$$\nabla_{365} x_t = x_t - x_{t-365}$$

公式解释：

• $\nabla_{365}$：365天周期的差分算子
• $x_t$：今年第$t$天的销量
• $x_{t-365}$：去年同期的销量
  操作意义：计算"今年第t天销量减去去年第t天销量"，消除固定年度季节性效应。

移动平均（Moving Average）

目的

平滑数据、去除随机噪声、凸显长期趋势。

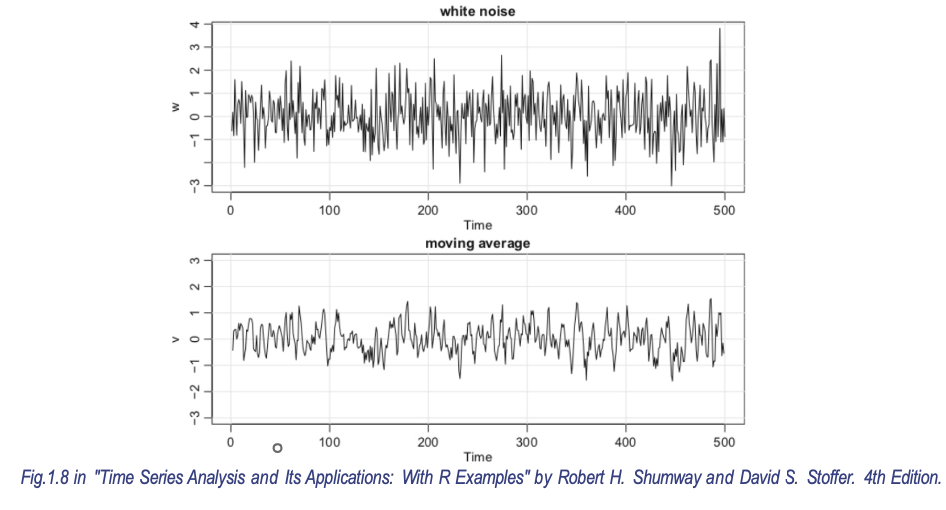
计算原理

$k$期移动平均：

$$\text{MA}_t = \frac{1}{k} \sum_{i=0}^{k-1} x_{t-i}$$

计算示例

原始序列：$[100, 102, 101, 105, 103]$

3日移动平均：

• $t=3$：$\frac{100 + 102 + 101}{3} = 101$

• $t=4$：$\frac{102 + 101 + 105}{3} \approx 102.67$

• $t=5$：$\frac{101 + 105 + 103}{3} = 103$

输出序列：$[-, -, 101, 102.67, 103]$

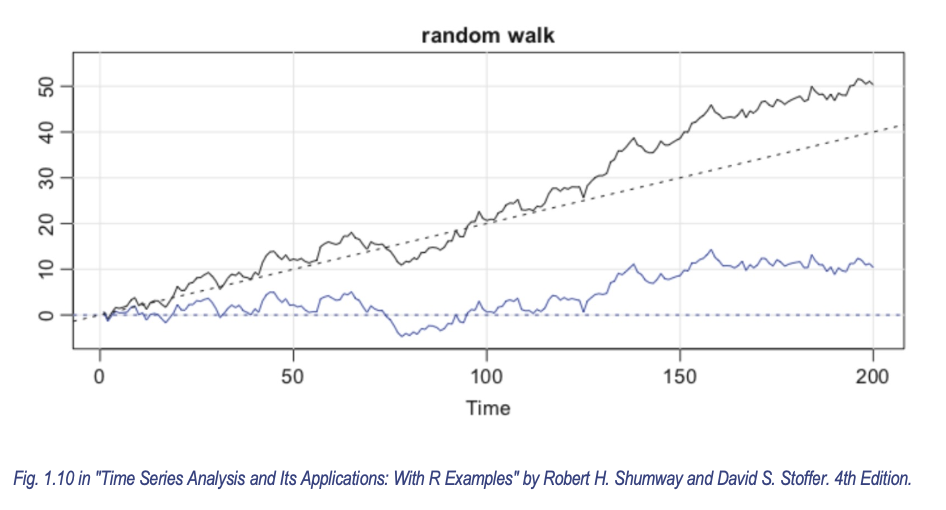
带漂移的随机游走（Random Walk with Drift）

基本模型

$$x_t = \delta + x_{t-1} + \omega_t$$

公式解释：

• $x_t$：时间$t$的值
• $\delta$：漂移项（常数）
• $\omega_t$：白噪声（均值为0，方差恒定）

模型推导

递归展开：

$$\begin{align*} x_t &= \delta + x_{t-1} + \omega_t \\ &= \delta + (\delta + x_{t-2} + \omega_{t-1}) + \omega_t \\ &= 2\delta + x_{t-2} + \omega_{t-1} + \omega_t \\ &\ \ \vdots \\ &= \delta \cdot t + \sum_{j=1}^{t} \omega_j \end{align*}$$

物理意义

类比说明：

• 随机游走（$\delta=0$）：醉汉每一步方向随机（抛硬币决定）
• 漂移项（$\delta \neq 0$）：醉汉被绳子持续向北轻拉（$\delta$为拉力）
• 整体路径：向北拉力($\delta t$) + 随机步长($\sum \omega_j$)

差分形式

$$\nabla x_t = x_t - x_{t-1} = \delta + \omega_t$$

关键结论：差分后转化为含常数项($\delta$)的白噪声，序列变为平稳。

信号与噪声

模型: $x_t = A\cos(2\pi\omega t + \Phi) + w_t$

这个模型表示观测到的时间序列是由一个 underlying signal（ underlying signal，如季节性成分 $A\cos(2\pi\omega t + \Phi)$）和叠加在上面的噪声（$w_t$）组成的。分析的目的是从噪声中提取出信号。

依赖性的度量

均值函数

用于描述时间序列在任意时刻 $t$ 的平均水平。

$$\mu_t = E(x_t) = \int_{-\infty}^{\infty} x f_t(x) dx \quad \text{(provided it exists)}$$

例子:

1. 对于移动平均 $v_t = \frac{1}{3}(w_{t-1} + w_t + w_{t+1})$，有 $E(v_t) = 0$。

2. 对于带漂移的随机游走 $x_t = \delta t + \sum_{j=1}^{t} w_j$，有 $E(x_t) = \delta t$。

3. 对于含信号的序列 $x_t = A\cos(2\pi\omega t + \phi) + w_t$，有 $E(x_t) = A\cos(2\pi\omega t + \phi)$。

自协方差函数

自协方差函数用于量化时间序列中当前值与过去值之间的线性相关性，反映了序列内部的动态依赖关系。核心问题是：一个变量在某个时刻的变化，是否可以用另一个时刻的变化来预测？

定义为：

$$\gamma(s, t) = \operatorname{Cov}(x_s, x_t) = E\left[(x_s - \mu_s)(x_t - \mu_t)\right]$$

• 衡量同一序列在不同时间点 $s$ 和 $t$ 的线性依赖性。

• $\gamma(s, t) = 0$ 表示 $x_t$ 和 $x_s$ 没有线性关系。

• 当 $s = t$ 时，$\gamma(t, t) = \operatorname{Var}(x_t)$。

例子:

1. 白噪声 $\{w_t\}$:

   $$\gamma(s, t) = \operatorname{cov}(w_s, w_t) = \begin{cases}\sigma_{w}^{2} & s=t \\ 0 & s\neq t \end{cases}$$

2. 3项移动平均 $v_t = \frac{1}{3}(w_{t-1} + w_t + w_{t+1})$:

   $$\gamma(s, t) = \begin{cases} \frac{3}{9}\sigma_{w}^{2} & s=t, \\ \frac{2}{9}\sigma_{w}^{2} & |s-t|=1, \\ \frac{1}{9}\sigma_{w}^{2} & |s-t|=2, \\ 0 & |s-t|>2 \end{cases}$$

3. 随机游走 $x_t = \sum_{j=1}^{t} w_j$:

   $$\gamma(s, t) = \operatorname{cov}(x_s, x_t) = \operatorname{cov}\left(\sum_{j=1}^{s} w_j, \sum_{k=1}^{t} w_k\right) = \min\{s, t\}\sigma_{w}^{2}$$