#sdsc6012

English / 中文

平稳性（Stationarity）

严格平稳性（Strict Stationarity）

时间序列 {xt}\{x_t\} 是严格平稳的，当且仅当对于任意 kk、任意时间点 t1,t2,…,tkt_1, t_2, \ldots, t_k 和任意时间偏移量 hh，都有：

P{xt1≤c1,…,xtk≤ck}=P{xt1+h≤c1,…,xtk+h≤ck}P\{x_{t_1} \leq c_1, \ldots, x_{t_k} \leq c_k\} = P\{x_{t_1+h} \leq c_1, \ldots, x_{t_k+h} \leq c_k\}

核心意义：严格平稳性意味着时间序列的完整概率分布不随时间变化。无论选择哪个时间窗口，其联合分布特性保持不变。这使得从单个时间序列样本中获取的统计量能够成为总体性质的有效估计。

弱平稳性（Weak Stationarity）

时间序列 {xt}\{x_t\} 是弱平稳的，如果满足：

  1. μt=E[xt]\mu_t = E[x_t] 是常数（与时间 tt 无关）

  2. γ(t+h,t)=Cov⁡(xt+h,xt)\gamma(t+h, t) = \operatorname{Cov}(x_{t+h}, x_t) 只依赖于时间间隔 hh，而与具体时间点 tt 无关

实际意义：弱平稳性只要求一阶矩（均值）和二阶矩（方差、协方差） 稳定，不要求完整的概率分布稳定。这使得"预测"成为可能，因为统计特性不随时间变化。

特征 严格平稳性 弱平稳性
核心定义 对于任意时间点集 t₁, t₂, …, tₙ 和任意时间平移 k，其联合分布满足：
F_{X_{t₁},…,X_{tₙ}}(x₁,…,xₙ) = F_{X_{t₁+k},…,X_{tₙ+k}}(x₁,…,xₙ)
（所有有限维联合分布保持不变）		 1. E[Xₜ] = μ（常数）
2. Cov(Xₜ, Xₜ₊ₖ) = γ(k)（仅依赖于滞后 k，不依赖于时间 t）
均值 未显式要求，但作为推论，若存在则必为常数：E[Xₜ] = μ（对所有 t 为常数） 明确要求：E[Xₜ] = μ（对所有 t 为常数）
方差 未显式要求，但作为推论，若存在则必为常数：Var(Xₜ) = σ²（对所有 t 为常数） 未直接要求，但由于协方差仅依赖于滞后，方差自然恒定：Var(Xₜ) = γ(0)（常数）
关注焦点 完整的概率分布 仅前两阶矩（均值、方差、协方差）

自协方差函数性质

对于平稳过程，自协方差函数 γ(h)\gamma(h) 满足：

  1. γ(0)≥0\gamma(0) \geq 0（方差非负）

  2. ∣γ(h)∣≤γ(0)|\gamma(h)| \leq \gamma(0)（自协方差绝对值不超过方差）

  3. γ(h)=γ(−h)\gamma(h) = \gamma(-h)（偶函数）

自相关函数（ACF）

ρ(h)=γ(h)γ(0)=Cov⁡(xt,xt+h)Var⁡(xt)=Corr(xt+h,xt)\rho(h) = \frac{\gamma(h)}{\gamma(0)} = \frac{\operatorname{Cov}(x_t, x_{t+h})}{\operatorname{Var}(x_t)}=Corr(x_{t+h}, x_t)

注：
γ(h)\gamma(h) 是自协方差函数，即 Cov(Xt,Xt+h)Cov(X_t, X_{t+h})。
γ(0)\gamma(0) 是该时间序列的方差，即 Var(Xt)Var(X_t)。

标准化意义：通过除以方差 γ(0)\gamma(0)，ACF的取值范围被约束到 [−1,1][-1, 1]，便于不同时间序列间的相关性强度比较。

时间序列分析

基本概念复习

对于时间序列观测值 x1,x2,…,xnx_{1}, x_{2}, \ldots, x_{n}，我们定义以下样本统计量：

  • 样本均值：

    xˉ=1n∑t=1nxt\bar{x} = \frac{1}{n} \sum_{t=1}^{n} x_{t}

    表示时间序列的平均水平。

  • 样本自协方差函数（sample autocovariance function）：
    对于滞后 hh（其中 h=0,1,2,…h = 0, 1, 2, \ldots），

    γ^(h)=1n∑t=1n−h(xt−xˉ)(xt+h−xˉ)\hat{\gamma}(h) = \frac{1}{n} \sum_{t=1}^{n-h} (x_{t} - \bar{x})(x_{t+h} - \bar{x})

    衡量时间序列中相隔 hh 个时间点的观测值之间的协方差。当 h=0h=0 时，就是样本方差。

  • 样本自相关函数（sample ACF）：

    ρ^(h)=γ^(h)γ^(0)\hat{\rho}(h) = \frac{\hat{\gamma}(h)}{\hat{\gamma}(0)}

    表示自协方差标准化后的值，范围在 [−1,1][-1, 1]，用于度量线性相关性。

简单示例计算

假设有一个简单的时间序列样本：[2,4,6,8][2, 4, 6, 8]，即 n=4n = 4。

  • 计算样本均值：

    xˉ=2+4+6+84=5\bar{x} = \frac{2 + 4 + 6 + 8}{4} = 5

  • 计算 γ^(0)\hat{\gamma}(0)（样本方差）：

    γ^(0)=14∑t=14(xt−5)2=14[(2−5)2+(4−5)2+(6−5)2+(8−5)2]=14(9+1+1+9)=5\begin{align*} \hat{\gamma}(0) & = \frac{1}{4} \sum_{t=1}^{4} (x_t - 5)^2 \\ & = \frac{1}{4} \left[ (2-5)^2 + (4-5)^2 + (6-5)^2 + (8-5)^2 \right] \\ & = \frac{1}{4} (9 + 1 + 1 + 9) \\ & = 5 \end{align*}

  • 计算 γ^(1)\hat{\gamma}(1)（滞后1的自协方差）：

    γ^(1)=14∑t=13(xt−5)(xt+1−5)=14[(2−5)(4−5)+(4−5)(6−5)+(6−5)(8−5)]=14[(−3)(−1)+(−1)(1)+(1)(3)]=14(3−1+3)=1.25\begin{align*} \hat{\gamma}(1) & = \frac{1}{4} \sum_{t=1}^{3} (x_t - 5)(x_{t+1} - 5) \\ & = \frac{1}{4} \left[ (2-5)(4-5) + (4-5)(6-5) + (6-5)(8-5) \right] \\ & = \frac{1}{4} \left[ (-3)(-1) + (-1)(1) + (1)(3) \right] \\ & = \frac{1}{4} (3 - 1 + 3) \\ & = 1.25 \end{align*}

白噪声过程的渐进性质

对于白噪声过程 wtw_t，如果 E[wt4]<∞E[w_t^4] < \infty，则样本ACF ρ^(h)\hat{\rho}(h) 满足：

  • ρ^(h)∼N(0,1/n)\hat{\rho}(h) \sim N(0, 1/n) 渐进分布

  • 对于 h≠0h \neq 0，ρ^(h)\hat{\rho}(h) 渐进服从均值为0、方差为 1/n1/n 的正态分布

实际意义：在大样本下，我们可以使用正态分布来检验ACF值的显著性，判断某个滞后项是否真正具有统计显著性。

公司销售数据案例分析

销售数据（24个月）：

Sales=[100,112,125,138,150,163,177,190,205,220,235,250,265,281,298,315,333,351,370,389,409,430,451,473]\begin{align*} \text{Sales} = [ & 100, 112, 125, 138, 150, 163, \\ & 177, 190, 205, 220, 235, 250, \\ & 265, 281, 298, 315, 333, 351, \\ & 370, 389, 409, 430, 451, 473] \end{align*}

  • 使用Python进行ACF分析：
    代码利用statsmodels库绘制ACF图和计算ACF值。

    • plot_acf函数生成自相关图，acf函数计算具体值。
    • 输出包括前10个滞位的ACF值，例如Lag0:1.0000, Lag1:高值（由于增长趋势），等。

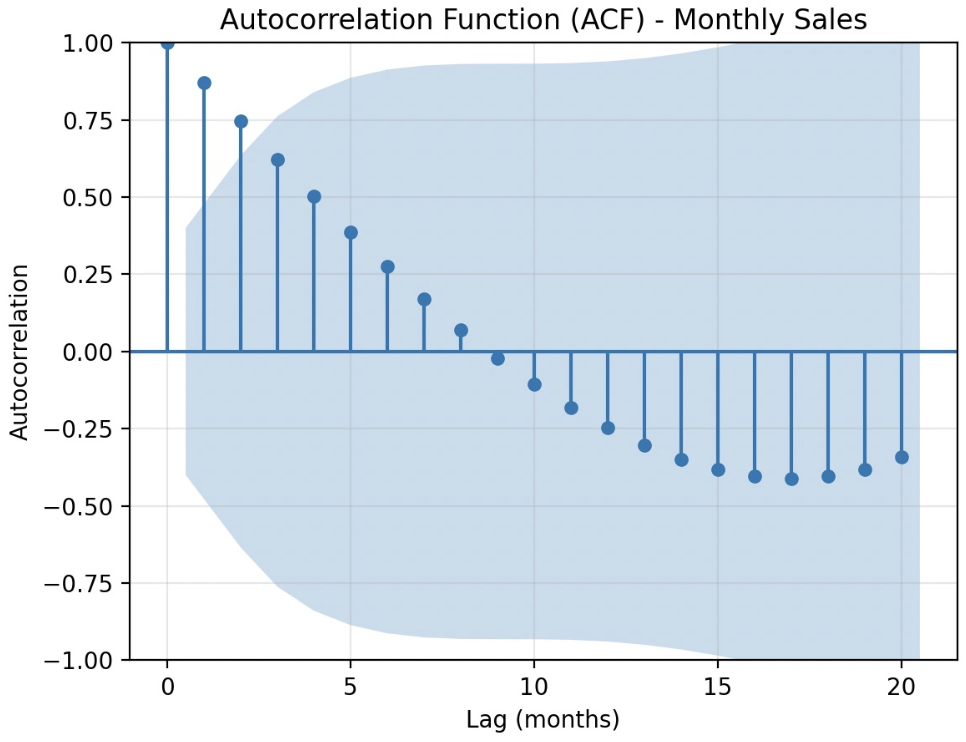
截屏2025-10-10 14.47.46.png

时间序列算子

后移算子（Backshift Operator）

  • 定义：Bxt=xt−1B x_t = x_{t-1}

  • 多次应用：Bkxt=xt−kB^k x_t = x_{t-k}（向后移动k个时间单位）

示例：假设有时间序列：x1=5,x2=8,x3=6,x4=9,x5=7x_1 = 5, x_2 = 8, x_3 = 6, x_4 = 9, x_5 = 7

  • Bx3=x2=8B x_3 = x_2 = 8

  • B2x4=x2=8B^2 x_4 = x_2 = 8

  • Bx5=x4=9B x_5 = x_4 = 9

前移算子（Forward-shift Operator）

  • 定义：Fxt=xt+1F x_t = x_{t+1}

  • 多次应用：Fkxt=xt+kF^k x_t = x_{t+k}（向前移动k个时间单位）

  • 关系：F=B−1F = B^{-1}，xt=B−1xt−1x_t = B^{-1} x_{t-1}

示例：使用相同序列：x1=5,x2=8,x3=6,x4=9,x5=7x_1 = 5, x_2 = 8, x_3 = 6, x_4 = 9, x_5 = 7

  • Fx2=x3=6F x_2 = x_3 = 6

  • F2x1=x3=6F^2 x_1 = x_3 = 6

  • Fx4=x5=7F x_4 = x_5 = 7

一阶差分算子（消除线性趋势）

定义与计算

  • 定义：∇xt=(1−B)xt\nabla x_t = (1 - B) x_t

  • 计算：∇xt=xt−xt−1\nabla x_t = x_t - x_{t-1}（计算连续观测值之间的变化）

工作原理分析

  1. 当前值成分：1⋅xt=xt1 \cdot x_t = x_t

  2. 前值成分：−Bxt=−xt−1-B x_t = -x_{t-1}

  3. 组合效果：(1−B)xt=xt−xt−1(1 - B) x_t = x_t - x_{t-1}

完整计算示例

时间(t) 观测值(xₜ) 差分计算过程 差分结果(∇xₜ)
1 10 - 缺失
2 12 12 - 10 = 2 2
3 14 14 - 12 = 2 2
4 16 16 - 14 = 2 2
5 18 18 - 16 = 2 2

结果分析：差分后的序列为 [缺失, 2, 2, 2, 2]，常数差分值表明原序列具有完美的线性趋势。

d阶差分算子（消除高阶趋势）

  • 定义：∇d=(1−B)d\nabla^d = (1 - B)^d

  • 应用：用于消除多项式趋势，d阶差分可以消除d次多项式趋势

差分算子的趋势消除能力实证

线性趋势消除的数学证明

当时间序列具有线性趋势：xt=β0+β1t+ytx_t = \beta_0 + \beta_1 t + y_t

一阶差分计算过程：

∇xt=xt−xt−1=(β0+β1t+yt)−(β0+β1(t−1)+yt−1)=β1+yt−yt−1\begin{aligned} \nabla x_t &= x_t - x_{t-1} \\ &= (\beta_0 + \beta_1 t + y_t) - (\beta_0 + \beta_1 (t-1) + y_{t-1}) \\ &= \beta_1 + y_t - y_{t-1} \end{aligned}

结论：线性趋势项 β1t\beta_1 t 被完全消除，只剩下常数项 β1\beta_1 和平稳成分的差分。

二次趋势消除的数学证明

当时间序列具有二次趋势：xt=β0+β1t+β2t2+ytx_t = \beta_0 + \beta_1 t + \beta_2 t^2 + y_t

一阶差分结果：

∇xt=β1−β2+2β2t+yt−yt−1\nabla x_t = \beta_1 - \beta_2 + 2\beta_2 t + y_t - y_{t-1}

二阶差分计算：

∇2xt=∇(∇xt)=(2β2t+β1−β2+yt−yt−1)−(2β2(t−1)+β1−β2+yt−1−yt−2)=2β2+yt−2yt−1+yt−2\begin{aligned} \nabla^2 x_t &= \nabla(\nabla x_t) \\ &= (2\beta_2 t + \beta_1 - \beta_2 + y_t - y_{t-1}) - (2\beta_2 (t-1) + \beta_1 - \beta_2 + y_{t-1} - y_{t-2}) \\ &= 2\beta_2 + y_t - 2y_{t-1} + y_{t-2} \end{aligned}

结论：二次趋势被完全消除，只剩下常数项 2β22\beta_2 和平稳成分的二阶差分。

线性过程（Linear Process）

定义

时间序列 {xt}\{x_t\} 称为线性过程，如果它可以表示为：

xt=μ+∑j=−∞∞ψjwt−jx_t = \mu + \sum_{j=-\infty}^{\infty} \psi_j w_{t-j}

其中：

  • {wt}∼wn⁡(0,σw2)\{w_t\} \sim \operatorname{wn}(0, \sigma_w^2)（白噪声过程）

  • μ\mu 是过程的均值

  • ψj\psi_j 是权重系数，满足绝对可和性：∑j=−∞∞∣ψj∣<∞\sum_{j=-\infty}^{\infty} |\psi_j| < \infty

组成部分分析

  • 因果部分：j≥0j \geq 0，表示当前值依赖于现在和过去的冲击

  • 非因果部分：j<0j < 0，表示当前值依赖于未来的冲击

  • 绝对可和条件：∑∣ψj∣<∞\sum |\psi_j| < \infty 保证了权重系数最终衰减到零：lim⁡∣j∣→∞∣ψj∣=0\lim_{|j|\to\infty} |\psi_j| = 0

与AR模型的关系

重要结论：所有平稳AR模型都是线性过程的特例，但并非所有线性过程都是AR模型。AR模型通过自身的过去值来存储"记忆"，而线性过程则通过白噪声冲击的加权和来表达。

线性过程与自回归模型（AR）

核心关系

线性过程和自回归模型之间的关系可以概括为：

“所有（平稳的）AR模型都是线性过程，但并非所有线性过程都是AR模型。”

示例说明

  • 线性过程：像一个广阔的"模型家族"，包含各种类型的模型

  • AR模型：是这个家族中一个"特定且广泛使用的成员"

关键区别：

  • AR模型将"记忆"存储在自身的历史值中（xt−1,xt−2,...x_{t-1}, x_{t-2}, ...）

  • 通过历史观测值的线性组合来定义当前值

自回归模型（AR）

直观理解

AR模型的核心理念：时间序列的当前值 xtx_t 可以通过其过去 pp 个值的线性组合来解释。

数学表达：

xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+wtx_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + w_t

其中：

  • ϕ1,ϕ2,...,ϕp\phi_1, \phi_2, ..., \phi_p 是自回归系数

  • wtw_t 是白噪声项（当前时刻的随机冲击）

不同阶数的AR模型示例

AR(1) 模型（一阶自回归）

模型形式：

今日温度=ϕ1×昨日温度+随机冲击今日温度 = \phi_1 \times 昨日温度 + 随机冲击

实际意义：只考虑昨天对今天的影响

具体示例：假设 ϕ1=0.8\phi_1 = 0.8，则：

今日温度=0.8×昨日温度+随机波动今日温度 = 0.8 \times 昨日温度 + 随机波动

AR(2) 模型（二阶自回归）

模型形式：

今日温度=ϕ1×昨日温度+ϕ2×前日温度+随机冲击今日温度 = \phi_1 \times 昨日温度 + \phi_2 \times 前日温度 + 随机冲击

实际意义：同时考虑昨天和前天的综合影响

具体示例：假设 ϕ1=0.6\phi_1 = 0.6, ϕ2=0.3\phi_2 = 0.3，则：

今日温度=0.6×昨日温度+0.3×前日温度+随机波动今日温度 = 0.6 \times 昨日温度 + 0.3 \times 前日温度 + 随机波动

实际应用示例

股票市场价格预测

假设某股票日收盘价遵循AR(2)模型：

今日股价=0.6×昨日股价+0.3×前日股价+随机波动今日股价 = 0.6 \times 昨日股价 + 0.3 \times 前日股价 + 随机波动

这表示：

  • 今日股价的60%受昨日股价影响

  • 30%受前日股价影响

  • 剩余10%来自随机波动

适用场景：AR模型适合具有趋势的数据，即当前值依赖于过去观测值的情况

算子表示法

后移算子（Backshift Operator）

  • 定义：Bxt=xt−1B x_t = x_{t-1}

  • 多次应用：

    • B2xt=xt−2B^2 x_t = x_{t-2}（向后移动2步）
    • Bpxt=xt−pB^p x_t = x_{t-p}（向后移动p步）

AR模型的算子形式

将AR(p)模型：

xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+wtx_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + w_t

转换为：

(1−ϕ1B−ϕ2B2−⋯−ϕpBp)xt=wt(1 - \phi_1 B - \phi_2 B^2 - \cdots - \phi_p B^p) x_t = w_t

定义自回归算子：

ϕ(B)=1−ϕ1B−ϕ2B2−⋯−ϕpBp\phi(B) = 1 - \phi_1 B - \phi_2 B^2 - \cdots - \phi_p B^p

最终得到简洁形式：

ϕ(B)xt=wt\phi(B) x_t = w_t

算子解释

ϕ(B)\phi(B) 不仅仅是一个缩写，它代表一个系统或滤波器：

  • 输入：原始时间序列 xtx_t

  • 系统：ϕ(B)\phi(B)（由参数 ϕ1,ϕ2,...,ϕp\phi_1, \phi_2, ..., \phi_p 定义）

  • 输出：白噪声 wtw_t

含义：如果我们将原始序列通过这个ϕ(B)\phi(B)系统滤波，所有可以被过去值捕获的可预测模式都将被移除，最终输出纯随机白噪声。

AR(1)模型的详细分析

模型形式

xt=ϕxt−1+wtx_t = \phi x_{t-1} + w_t

求解过程

通过连续代入：

xt=ϕxt−1+wt=ϕ(ϕxt−2+wt−1)+wt=ϕ2xt−2+ϕwt−1+wtx_t = \phi x_{t-1} + w_t = \phi(\phi x_{t-2} + w_{t-1}) + w_t = \phi^2 x_{t-2} + \phi w_{t-1} + w_t

继续此过程n次：

xt=ϕnxt−n+∑j=0n−1ϕjwt−jx_t = \phi^n x_{t-n} + \sum_{j=0}^{n-1} \phi^j w_{t-j}

算子解法

使用后移算子：(1−ϕB)xt=wt(1 - \phi B) x_t = w_t

应用逆算子（当 ∣ϕ∣<1|\phi| < 1 时有效）：

xt=(1−ϕB)−1wt=∑j=0∞ϕjBjwt=∑j=0∞ϕjwt−jx_t = (1 - \phi B)^{-1} w_t = \sum_{j=0}^{\infty} \phi^j B^j w_t = \sum_{j=0}^{\infty} \phi^j w_{t-j}

因果性与平稳性

因果过程

时间序列过程称为因果的，如果其当前值仅依赖于：

  • 现在和过去的输入/冲击过程

  • 不依赖于未来值

AR(1)模型的因果性条件

AR(1)过程 xt=ϕxt−1+wtx_t = \phi x_{t-1} + w_t 是因果的当且仅当：

条件1：∣ϕ∣<1|\phi| < 1

条件2：多项式 ϕ(z)=1−ϕz\phi(z) = 1 - \phi z 的根 z1z_1 满足 ∣z1∣>1|z_1| > 1

当 ∣ϕ∣<1|\phi| < 1 时：过程可以表示为 xt=∑j=0∞ϕjwt−jx_t = \sum_{j=0}^{\infty} \phi^j w_{t-j}，仅依赖于过去和现在的噪声

非因果情况

当 ∣ϕ∣>1|\phi| > 1 时，过程是非因果的，依赖于未来噪声：

xt=−∑j=1∞ϕ−jwt+jx_t = -\sum_{j=1}^{\infty} \phi^{-j} w_{t+j}

AR(p)模型的平稳性条件

AR(p)模型存在平稳解当且仅当自回归特征多项式：

ϕ(z)=1−ϕ1z−ϕ2z2−⋯−ϕpzp=0\phi(z) = 1 - \phi_1 z - \phi_2 z^2 - \cdots - \phi_p z^p = 0

的所有根都在单位圆外（即所有根的模大于1）。

实例：检查因果性

示例1：AR(2)模型

考虑模型：xt=1.5xt−1−0.5xt−2+wtx_t = 1.5x_{t-1} - 0.5x_{t-2} + w_t

特征多项式：ϕ(z)=1−1.5z+0.5z2\phi(z) = 1 - 1.5z + 0.5z^2

解方程：1−1.5z+0.5z2=01 - 1.5z + 0.5z^2 = 0得根：z1=1z_1 = 1, z2=2z_2 = 2

由于 ∣z1∣=1|z_1| = 1（在单位圆上），该过程不是因果的。

示例2：AR(2)模型

考虑模型：xt=0.5xt−1+0.2xt−2+wtx_t = 0.5x_{t-1} + 0.2x_{t-2} + w_t

特征多项式：ϕ(z)=1−0.5z−0.2z2\phi(z) = 1 - 0.5z - 0.2z^2

解方程得根：z1≈−1.35z_1 \approx -1.35, z2≈3.70z_2 \approx 3.70

由于 ∣z1∣≈1.35>1|z_1| \approx 1.35 > 1 且 ∣z2∣≈3.70>1|z_2| \approx 3.70 > 1，该过程是因果的。