#sdsc6015
English / 中文
课程介绍与随机优化初步
主问题 / Main Problem
给定带标签训练数据 (x1,y1),…,(xn,yn)∈Rd×Y,
寻找权重 θ 以最小化:
θminf(θ)=n1i=1∑nℓ(θ,(xi,yi)),n 极大
目标:通过损失函数 ℓ 衡量模型预测误差,优化参数 θ。
补充说明 / Supplementary Notes
数学符号解释:
-
θ∈Rm:待优化参数向量(例如线性模型的权重、神经网络的参数)
-
ℓ(θ,(xi,yi)):损失函数,量化模型预测 y^i=gθ(xi) 与真实标签 yi 的差异
-
n1∑i=1n:经验风险,表示在训练集上的平均损失
实际意义:
该优化问题称为经验风险最小化 (ERM):
- 核心思想:通过最小化训练集上的平均损失,使模型泛化到新数据
- 挑战:当 n 极大时,直接计算整个数据集的梯度计算成本过高
- 解决方案:随机优化算法(如SGD)每次迭代仅用部分数据近似梯度
软间隔支持向量机 / Soft Margin SVM

w,bmin{n1i=1∑nmax(0,1−yi(w⊤xi−b))+λ∥w∥2}
合页损失 (Hinge Loss):max(0,1−yi(w⊤xi−b)) 惩罚分类错误。
正则化 (Regularization):λ∥w∥2 控制模型复杂度,防止过拟合。
补充说明 / Supplementary Notes
数学原理推导:
-
合页损失的来源:
- 理想约束 yi(w⊤xi−b)≥1(所有样本正确分类且间隔至少为1)
- 引入松弛变量 ξi≥0 允许违反约束:yi(w⊤xi−b)≥1−ξi
- 最小化违反程度 ∑ξi → max(0,1−yi(w⊤xi−b))
几何意义:样本到决策边界的距离 d=∥w∥∣w⊤xi−b∣,当 d<∥w∥1 时被惩罚
-
正则化项的推导:
- 间隔大小 M=∥w∥2
- 最大化间隔等价于最小化 ∥w∥2(因 argmaxM=argmin∥w∥)
实际意义:λ 平衡分类误差与模型复杂度
- λ→0:允许更多误分类(大间隔)
- λ→∞:严格分类(小间隔)
符号扩展解释:
示例:
二维空间中:
示例:图像去噪 / Example: Image Denoising
全变分去噪模型 (Total Variation Denoising Model):
Xmin(i,j)∈P∑∣Xij−Oij∣2+λ⋅TV(X)
-
X:待恢复图像矩阵
-
O:含噪观测图像
-
P:观测像素索引集
-
TV(X):全变分正则项:
TV(X)=i,j∑∣Xi+1,j−Xij∣+∣Xi,j+1−Xij∣
数据保真项 (Data Fidelity):∑∣Xij−Oij∣2 确保恢复图像接近观测值。
平滑约束 (Smoothness):TV(X) 通过惩罚相邻像素差异,促进分段平滑。
补充说明 / Supplementary Notes
数学原理推导:
-
全变分项 TV(X) 的物理意义:
- ∣Xi+1,j−Xij∣ 计算垂直方向梯度(像素与下方邻居的强度差)
- ∣Xi,j+1−Xij∣ 计算水平方向梯度(像素与右侧邻居的强度差)
核心思想:自然图像具有"分段平滑"特性(相邻像素相似),而噪声破坏这种连续性
-
优化目标分解:
- 数据保真项:最小化 ∥X−O∥F2(Frobenius范数平方)→ 保持与观测图像相似
- 正则化项:最小化图像梯度 ∥∇X∥1(梯度向量的L1范数)→ 促进平滑
λ 控制平滑强度:λ↑ → 更平滑但可能模糊细节
符号扩展解释:
-
Xij∈[0,255]:图像在位置 (i,j) 的像素强度(灰度值)
-
∇X=[Xi+1,j−XijXi,j+1−Xij]:离散梯度算子
-
L1范数 ∥∇X∥1:对噪声更鲁棒(相比L2范数)
实际意义:
示例:
假设 2×2 噪声图像 O=[503010080]:
-
计算 TV(O)=∣50−30∣+∣50−100∣+∣30−80∣+∣100−80∣=20+50+50+20=140
-
去噪后图像 X 的 TV(X) 值显著降低(如降为40),同时 ∣X−O∣2 保持较小
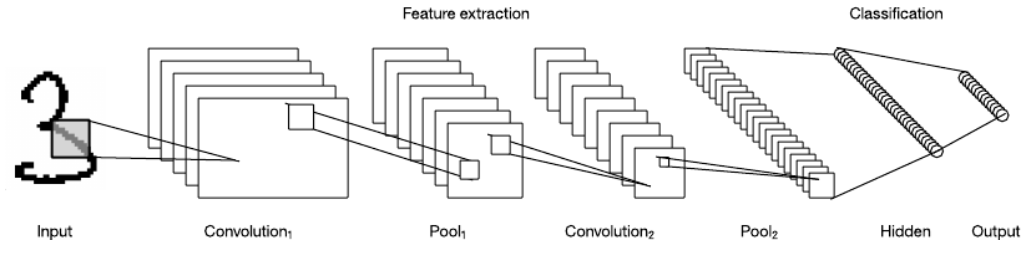
示例:神经网络 / Example: Neural Networks
卷积神经网络 (Convolutional Neural Network):
w,bminf(w,b)=n1i=1∑nℓ(w,b,(xi,yi))
其中
ℓ(w,b,(xi,yi))=w3⊤⋅Q(w2⊤⋅Q(w1⊤xi−b1)−b2)−yi2
-
Q(w)i=max(0,wi):ReLU激活函数
-
w1,w2,w3:权重矩阵
-
b1,b2:偏置向量
-
xi:输入数据,yi:目标输出
ReLU激活:Q(⋅) 对负输入输出0,引入非线性。
层级结构:嵌套变换 wk⊤⋅Q(⋅)−bk 建模复杂特征交互。
补充说明 / Supplementary Notes
数学原理推导:
-
前向传播过程:
- 输入层:xi∈Rd0(原始输入,如图像像素)
- 隐藏层1:z(1)=w1⊤xi−b1(线性变换)
a(1)=Q(z(1))(ReLU激活,max(0,z(1)))
- 隐藏层2:z(2)=w2⊤a(1)−b2
a(2)=Q(z(2))
- 输出层:y^i=w3⊤a(2)(预测值)
ℓ=∥y^i−yi∥2 计算预测与真实值的平方误差
-
ReLU的数学特性:
Q(z)={z0if z>0otherwise
优势:
- 解决梯度消失问题(正区间梯度恒为1)
- 稀疏激活(约50%神经元激活)
符号扩展解释:
-
wk∈Rdk×dk−1:权重矩阵(dk为第k层神经元数)
-
bk∈Rdk:偏置向量(平移决策边界)
-
Q(⋅):逐元素操作(对向量/矩阵中每个元素独立应用ReLU)
实际意义:
-
特征提取:
- 浅层学习边缘/纹理(w1)
- 中层学习部件/形状(w2)
- 高层学习语义概念(w3)
-
优化挑战:
- 非凸目标函数(存在多个局部最优)
- 梯度计算需反向传播(链式法则)
示例(数字识别):
输入 xi 为28×28手写数字图像(d0=784):
-
w1:卷积核提取边缘(输出 d1=32 特征图)
-
Q:保留正激活(增强特征对比度)
-
w2:组合边缘为数字部件(如"7"的横折)
-
w3:组合部件为数字0-9(输出 d3=10)
简单数值示例:最小二乘回归 / Simple Numerical Example: Least Squares Regression
问题描述 / Problem Setup
xminf(x):=21∥Ax−y∥2
-
A∈Rn×d:数据矩阵
-
y∈Rn:观测向量
-
x∈Rd:待优化变量
梯度下降 vs. 随机梯度下降 / Gradient Descent (GD) vs. Stochastic Gradient Descent (SGD)
| 方法 |
更新规则 |
梯度计算 |
单步计算成本 |
| GD |
xt+1=xt−η∇f(xt) |
∇f(x)=A⊤(Ax−y) |
O(nd) |
| SGD |
xt+1=xt−η∇ft(xt) |
∇ft(x)=ai⊤(aix−yi) |
O(d) |
核心思想:
- GD 每步使用全部 n 个数据点 → 计算量大但收敛稳定。
- SGD 每步随机使用一个数据点 (ai,yi) → 计算高效,适合大规模数据,但收敛带噪声。
模拟参数 / Simulation Parameters
-
数据:A=121211, y=1.53.52.0 (n=3, d=2)
-
步长:η=0.1
-
初始值:x0=(0,0)
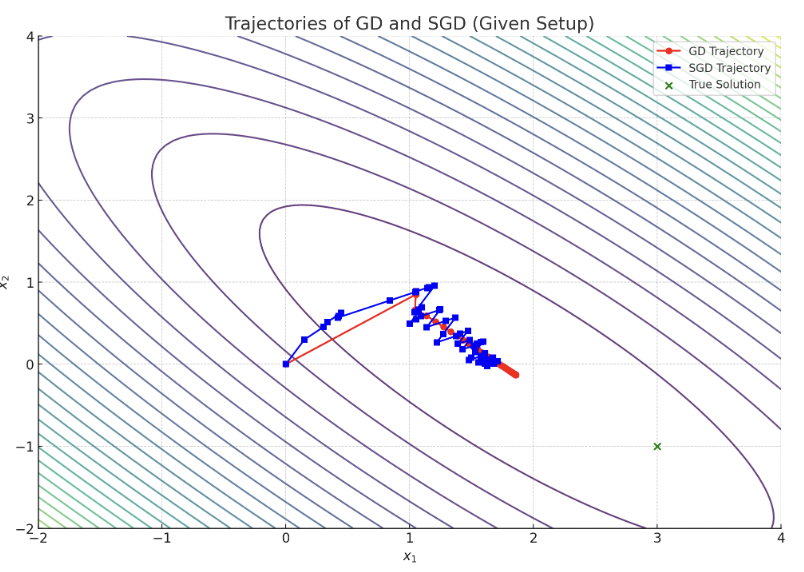

关键结论 / Key Takeaways
随机优化基础 (Preliminaries of Stochastic Optimization)
柯西-施瓦茨不等式 / Cauchy-Schwarz Inequality
对任意向量 u,v∈Rd:
∣u⊤v∣≤∥u∥∥v∥
符号说明:
-
u=u1⋮ud, v=v1⋮vd:d维实数列向量
-
u⊤v=∑i=1duivi:标量积(内积)
-
∥u∥=u⊤u=∑i=1dui2:欧几里得范数
几何解释:
- 单位向量情形(∥u∥=∥v∥=1)时,等式成立当且仅当 u=v 或 u=−v
- 可定义向量夹角 α:cosα=∥u∥∥v∥u⊤v,满足 −1≤cosα≤1

Examples for unit vectors (‖u‖=‖v‖= 1)

Equality in Cauchy-Schwarz if and only u = v or u = −v.
赫尔德不等式 / Hölder’s Inequality
对 p,q>1 满足 p1+q1=1,及任意向量 x,y:
i=1∑n∣xiyi∣≤(i=1∑n∣xi∣p)1/p(i=1∑n∣yi∣q)1/q
关联概念:
核心思想:通过 ℓp 和 ℓq 范数量化向量间相互作用的上界。
凸集 / Convex Sets
集合 C 是凸集当且仅当任意两点连线仍在 C 内:
∀x,y∈C, ∀λ∈[0,1],λx+(1−λ)y∈C
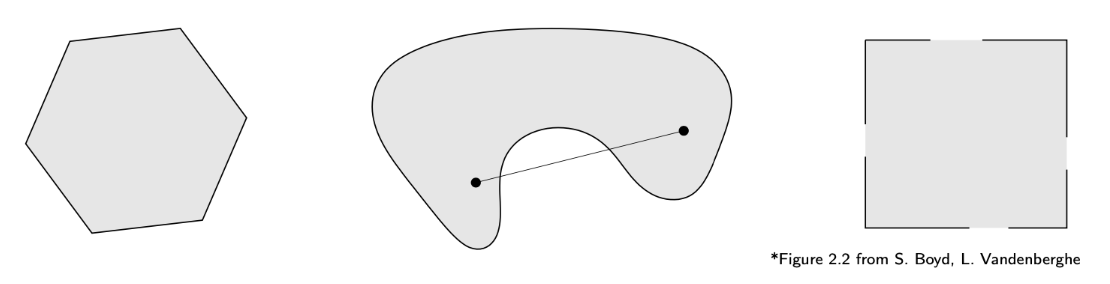
左图:凸集
中图:非凸集(线段不全在集合内)
右图:非凸集(部分边界点缺失)
凸集性质 / Properties
-
交运算封闭:凸集的交集仍是凸集
i∈I⋂Ci 凸,∀凸集 Ci

-
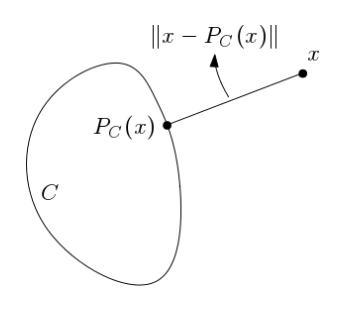
投影唯一性:对非空闭凸集 C,投影算子 PC(x)=argy∈Cmin∥y−x∥的解唯一
-
非扩张性:
∥PC(x)−PC(y)∥≤∥x−y∥,∀x,y

利普希茨连续性 / Lipschitz Continuity
函数 f:Rd→R 是 L-利普希茨连续的若:
∥f(x)−f(y)∥≤L∥x−y∥,∀x,y∈Rd
L 的意义:函数变化速率的上界
示例:f(x)=x2+5, f(x)=∥x∥
可微函数 / Differentiable Functions
函数 f:Rd→R 在 x0 可微若存在梯度 ∇f(x0) 使得:
f(x0+h)≈f(x0)+∇f(x0)⊤h
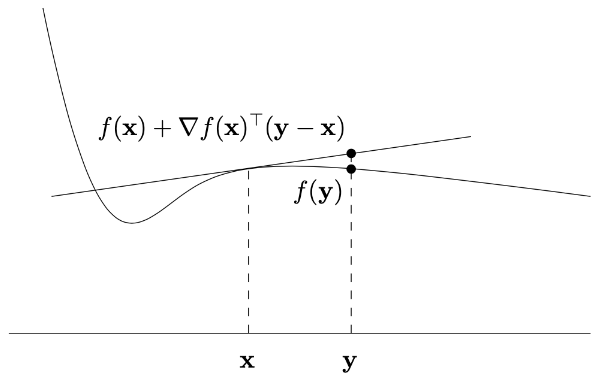
其中 h 为微小扰动。全域可微时,其图像每点均有切超平面。
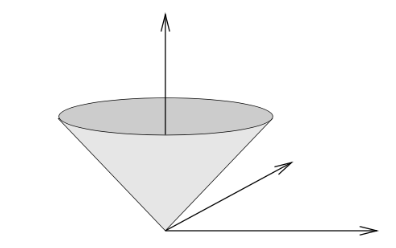
不可微函数示例
f(x)=∥x∥(欧几里得范数)

特性:在原点不可微("冰激凌锥"状图像)
L-光滑性 / L-Smoothness
函数 f:Rd→R 是 L-光滑的若:
-
f 连续可微(梯度 ∇f 存在且连续)
-
梯度满足 L-利普希茨条件:
∥∇f(x)−∇f(y)∥≤L∥x−y∥,∀x,y
梯度定义:
∇f(x)=(∂x1∂f(x),…,∂xd∂f(x))
示例:f(x)=21∥x∥2 是 1-光滑函数
补充说明 / Supplementary Notes
数学原理推导:
-
Lipschitz常数的计算:
L=x=ysup∥x−y∥∣f(x)−f(y)∣
即函数在任意两点间割线斜率的最大值
-
可微函数的Lipschitz条件:
若 f 可微,则 L=supx∥∇f(x)∥
证明:由中值定理 ∣f(x)−f(y)∣=∣∇f(ξ)⊤(x−y)∣≤∥∇f(ξ)∥∥x−y∥
符号扩展解释:
-
∥x−y∥:Rd 中两点间的欧氏距离
-
L:Lipschitz常数(函数变化率的上界)
-
∣f(x)−f(y)∣:函数值变化的绝对值
实际意义:
-
优化算法稳定性:
- 梯度下降法中,L 决定最大允许步长(η<2/L)
- 保证算法收敛性(防止振荡或发散)
-
神经网络训练:
- 权重矩阵的Lipschitz约束控制模型敏感性
- 提高对抗鲁棒性(抵抗输入扰动)
示例验证:
-
f(x)=∥x∥:
∣∥x∥−∥y∥∣≤∥x−y∥(三角不等式)
→ L=1
-
f(x)=x2+5:
dxdx2+5=x2+5∣x∣≤1
→ L=1
-
非Lipschitz函数:f(x)=x2
∣x−y∣∣x2−y2∣=∣x+y∣∣x∣,∣y∣→∞∞
→ 无全局Lipschitz常数
几何解释:
凸函数
定义与几何意义 / Definition and Geometric Interpretation
函数 f:Rd→R 是凸函数若:
-
定义域 dom(f) 是凸集
-
满足凸不等式:
∀x,y∈dom(f), ∀λ∈[0,1],f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)
几何解释:函数图像上任意两点的连线(弦)位于图像上方。

补充说明 / Supplementary Notes
数学符号解释:
-
λ∈[0,1]:插值参数,控制两点间的线性组合比例
-
λx+(1−λ)y:凸组合,表示连接 x 和 y 的线段上的点
-
f(λx+(1−λ)y):函数在凸组合点处的值
-
λf(x)+(1−λ)f(y):函数值在 f(x) 和 f(y) 间的线性插值
关键性质推导:
凸不等式可等价表述为:
∥y−x∥f(y)−f(x)≥∥z−x∥f(z)−f(x),∀z∈[x,y]
即函数在任意区间 [x,y] 上的平均增长率单调不减
实际意义:
几何特性详解:
-
弦在图像上方:
- 对任意 x,y,连接 (x,f(x)) 和 (y,f(y)) 的线段
- 始终位于函数图像 z=f(λx+(1−λ)y) 的上方
-
无局部凹陷:
- 函数曲线不会出现"碗状"凹陷(如 f(x)=−x2)
- 二阶可微时等价于 ∇2f(x)⪰0(Hessian矩阵半正定)
示例验证:
-
凸函数:f(x)=x2
f(λx+(1−λ)y)=[λx+(1−λ)y]2
λf(x)+(1−λ)f(y)=λx2+(1−λ)y2
差值:λ(1−λ)(x−y)2≥0 → 满足凸不等式
-
非凸函数:f(x)=sin(x)(在 [0,2π])
取 x=0,y=2π,λ=0.5:
f(0.5×0+0.5×2π)=sin(π)=0
0.5sin(0)+0.5sin(2π)=0
但 x=π/2 时 f(π/2)=1>0 → 违反凸不等式
比喻理解:
将凸函数想象成"山谷":
- 从任意两点出发的缆车线(弦)始终高于山谷底部(函数图像)
- 水滴沿山谷下滑时,最终必汇聚到最低点(全局最优)
常见凸函数示例 / Examples
-
线性函数:f(x)=a⊤x
-
仿射函数:f(x)=a⊤x+b
-
指数函数:f(x)=eαx
-
范数:任意 Rd 上的范数(如欧几里得范数 ∥x∥)
范数凸性证明:
由三角不等式 ∥x+y∥≤∥x∥+∥y∥ 和齐次性 ∥αx∥=∣α∣∥x∥:
∥λx+(1−λ)y∥≤λ∥x∥+(1−λ)∥y∥
凸函数与集合的关系 / Epigraph and Convexity
函数的图
函数的图定义为:
{(x,f(x))∣x∈dom(f)}
其中,dom(f) 表示函数 f 的定义域。
Epigraph(上镜图)
函数 f:Rd→R 的 epigraph 定义为:
epi(f):={(x,α)∈Rd+1∣x∈dom(f),α>f(x)}
补充说明:epigraph 是函数图像上方的所有点集,直观理解为函数“上方”的区域。例如,如果 f(x) 是凸函数,epigraph 会形成一个“碗状”凸集。
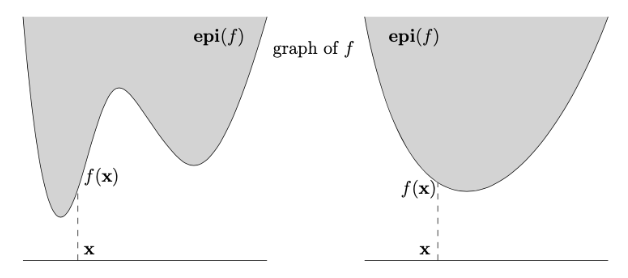
证明: f 是凸函数 ⟺ epi(f) 是凸集
⇒(充分性):假设 f 是凸函数。取任意点 (x,t),(y,s)∈epi(f),需证明线段 λ(x,t)+(1−λ)(y,s) 在 epi(f) 中,即:
f(λx+(1−λ)y)≤λt+(1−λ)s
由 f 的凸性(定义:f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)),且因为 (x,t),(y,s)∈epi(f) 有 t>f(x) 和 s>f(y),所以不等式成立。故 epi(f) 是凸集。
⇐(必要性):假设 epi(f) 是凸集。取点 (x,f(x)),(y,f(y))∈epi(f)。由于 epi(f) 凸,线段 λ(x,f(x))+(1−λ)(y,f(y)) 在 epi(f) 中,即:
(λx+(1−λ)y,λf(x)+(1−λ)f(y))∈epi(f)
由 epigraph 定义,λf(x)+(1−λ)f(y)>f(λx+(1−λ)y),这等价于 f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)。故 f 是凸函数。
补充说明:证明的核心是利用 epigraph 定义中的不等式 α>f(x),将集合凸性转化为函数凸性。第一部分从函数凸性推导集合凸性,第二部分反之。
Jensen不等式
引理1(Jensen不等式)
设 f 为凸函数,x1,…,xm∈dom(f),λ1,…,λm∈R+ 且满足 ∑i=1mλi=1,则:
f(i=1∑mλixi)≤i=1∑mλif(xi)
说明:
- 当 m=2 时,即为凸函数的定义:f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2)。
- 一般情况的证明可通过数学归纳法完成(留作练习)。核心思路是将 m 个点的凸组合拆分为两两组合的递归形式。
可微函数的几何性质
对于可微函数 f,其仿射函数:
f(x)+∇f(x)⊤(y−x)
的图形是函数 f 在点 (x,f(x)) 处的切线超平面。
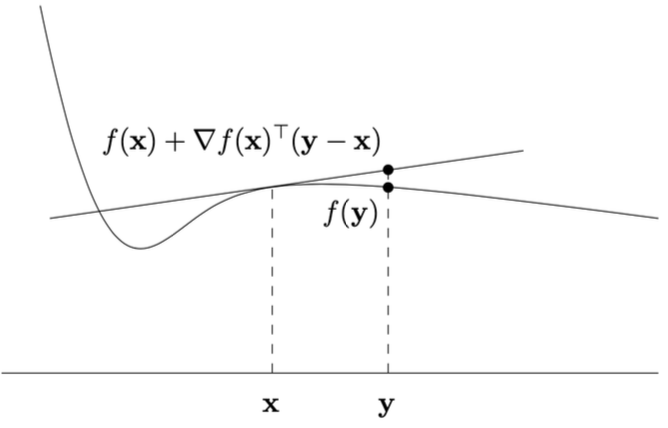
几何解释:
- ∇f(x) 是 f 在 x 处的梯度(多维导数)。
- 该切线超平面在 x 处与 f 的曲面相切,且是 f 在 x 附近的局部线性逼近。
- 若 f 是凸函数,该切线超平面位于整个函数的 epigraph 内(即切线在函数图像下方)。
凸性判据 / Convexity Criteria
一阶凸性判定
引理 2
设 dom(f) 为开集且 f 可微(梯度 ∇f(x):=(∂x1∂f(x),…,∂xd∂f(x)) 处处存在),则 f 是凸函数当且仅当:
-
dom(f) 是凸集;
-
对所有 x,y∈dom(f),满足:
f(y)≥f(x)+∇f(x)⊤(y−x)
几何解释:
- 该不等式表明凸函数的图像始终位于其任意一点的切线超平面之上(如图形为“碗状”)。
- 梯度 ∇f(x) 是函数在 x 处的最速上升方向,而 −∇f(x) 是最速下降方向。
二阶凸性判定
设 dom(f) 为开集且 f 二阶可微(Hessian 矩阵 ∇2f(x) 对称且处处存在),则 f 是凸函数当且仅当:
-
dom(f) 是凸集;
-
对所有 x∈dom(f),Hessian 矩阵半正定(∇2f(x)⪰0),即:
∀z∈Rd,z⊤∇2f(x)z≥0
关键概念:
- Hessian 矩阵:二阶偏导数构成的对称矩阵,描述函数的局部曲率:
∇2f(x)=∂x12∂2f⋮∂xd∂x1∂2f⋯⋱⋯∂x1∂xd∂2f⋮∂xd2∂2f
示例
函数 f(x1,x2)=x12+x22 的 Hessian 为:
∇2f(x)=(2002)⪰0
说明:该矩阵是正定矩阵(特征值均为 2 > 0),故 f 是严格凸函数(旋转抛物面)。
凸函数性质 / Properties
保凸运算
引理 4
(i) 设 f1,…,fm 为凸函数,λ1,…,λm∈R+,则函数 f:=∑i=1mλifi 在定义域 dom(f):=⋂i=1mdom(fi) 上是凸函数。
说明:凸函数的非负线性组合仍是凸函数(定义域取交集)。
(ii) 设 f 为凸函数(dom(f)⊆Rd),g(x)=Ax+b 是仿射映射(A∈Rd×m,b∈Rd),则复合函数 f∘g(即 x↦f(Ax+b))在 dom(f∘g):={x∈Rm:Ax+b∈dom(f)} 上是凸函数。
说明:凸函数与仿射映射的复合仍保持凸性(例如 f(2x+1) 是凸的)。
局部极小即全局极小
定义:f 的局部极小点 x 满足:存在 ε>0,使得对所有 ∥y−x∥≤ε 的 y∈dom(f),有 f(x)≤f(y)。
引理 5:凸函数 f 的局部极小点 x∗ 必为全局极小点(即 f(x∗)≤f(y),∀y∈dom(f))。
证明:
假设存在 y 使 f(y)<f(x∗)。构造点 y′=λx∗+(1−λ)y(λ∈(0,1))。由凸性:
f(y′)≤λf(x∗)+(1−λ)f(y)<f(x∗).
当 λ→1 时,∥y′−x∗∥→0,与 x∗ 是局部极小矛盾。
临界点即全局极小
引理 6:若 f 在开凸集 dom(f) 上可微且凸,且 ∇f(x)=0(临界点),则 x 是全局极小点。
证明:
由一阶凸性条件(引理 2),对任意 y:
f(y)≥f(x)+=0∇f(x)⊤(y−x)=f(x).
几何解释:梯度为零时,切线超平面水平,函数值全局最小。
严格凸函数
定义:f 是严格凸函数若:
-
dom(f) 凸;
-
对所有 x=y 和 λ∈(0,1):
f(λx+(1−λ)y)<λf(x)+(1−λ)f(y).

示例:
- x2 严格凸(左图);
- 线性函数凸但不严格凸(右图)。
引理 7:严格凸函数至多有一个全局极小点。
约束最小化
定义:设 f 凸,X⊆dom(f) 凸集。x∈X 是 f 在 X 上的极小点若 f(x)≤f(y),∀y∈X。
引理 8:若 f 在开凸集 dom(f) 上可微,X⊆dom(f) 凸,则 x∗∈X 是最小点当且仅当:
∇f(x∗)⊤(x−x∗)≥0,∀x∈X.

几何解释:在 x∗ 处,梯度方向与可行方向夹角 ≤90∘(即无下降方向)。
全局最小值的存在性
关键点:函数有下界仅说明值域存在下确界(infimum),但未必能在某点取到该值(即最小值)。
定义:α-下水平集
设函数 f:Rd→R 和实数 α∈R,定义其 α-下水平集为:
f≤α:={x∈Rd∣f(x)≤α}
 )
)
凸优化问题
形式:
x∈Dminf(x),
其中 f 凸,D⊆dom(f) 凸集(如 D=Rd)。
关键性质:
收敛速率示例:梯度下降的收敛速率为 O(1/t),即:
f(xt)−f(x∗)≤tc,
其中 x∗ 为最优解,c 为常数(依赖初始条件和函数性质)。

















 )
)
