#sdsc6015
English / 中文
回顾 - 凸函数与凸优化
点击展开
回顾
函数 f:Rd→R 是凸函数当且仅当:
-
定义域 dom(f) 是凸集;
-
对所有 x,y∈dom(f) 和 λ∈[0,1],满足:
f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)
几何意义:函数图像上任意两点间的线段位于图像上方。
回顾
若 f 可微,则凸性等价于:
f(y)≥f(x)+∇f(x)⊤(y−x),∀x,y∈dom(f)
几何意义:函数图像始终在其切超平面的上方。
回顾
-
定义:f 在 x0 可微当存在梯度 ∇f(x0) 使得:
f(x0+h)≈f(x0)+∇f(x0)⊤h
其中 h 为微小扰动。
-
全局可微:若在定义域内每点可微,则称 f 可微,其图像在各点有非垂直切超平面。
回顾
形式:
x∈Rdminf(x)
其中 f 是凸可微函数,Rd 是凸集。全局最小值点记为 x∗=argminf(x)(可能有多个)。
梯度下降法 (Gradient Descent)
核心思想
利用负梯度方向更新参数(梯度 ∇f(x) 指向函数值增长最快的方向):
xk+1=xk−ηk∇f(xk)
其中:
-
xk:当前迭代点的参数向量(k 为迭代次数)
-
ηk:步长(学习率),控制更新幅度(ηk>0)
-
∇f(xk):函数 f 在 xk 处的梯度
-
xk+1:更新后的参数向量
关键说明:
- 梯度方向:负梯度 −∇f(xk) 指向函数值下降最快的方向;
- 步长选择:
- 固定步长(如 ηk=0.1)需满足收敛条件;
- 自适应步长(如 ηk=k1)可提升收敛性;
- 几何意义:每次迭代沿当前点的梯度方向线性移动 ηk∥∇f(xk)∥ 的距离。
梯度下降示例:二次函数优化
考虑凸函数 f(x)=21x2:
梯度下降更新规则
固定步长 η 下的迭代公式:
xt+1=xt−η∇f(xt)=xt−ηxt=xt(1−η)
-
xt:第 t 次迭代的参数值
-
η:步长(学习率),控制更新幅度
迭代序列通式
经过 k 次迭代后:
xk=x0(1−η)k
推导说明:
由 xk=xk−1(1−η) 递归展开:
xk=xk−1(1−η)=xk−2(1−η)2=⋯=x0(1−η)k
收敛性分析
当步长满足 0<η<1 时:
k→∞limxk=k→∞limx0(1−η)k=0
解释:
由于 ∣1−η∣<1,序列 (1−η)k 指数衰减到 0,因此迭代点收敛到最小值点 x∗=0。
具体参数下的收敛行为
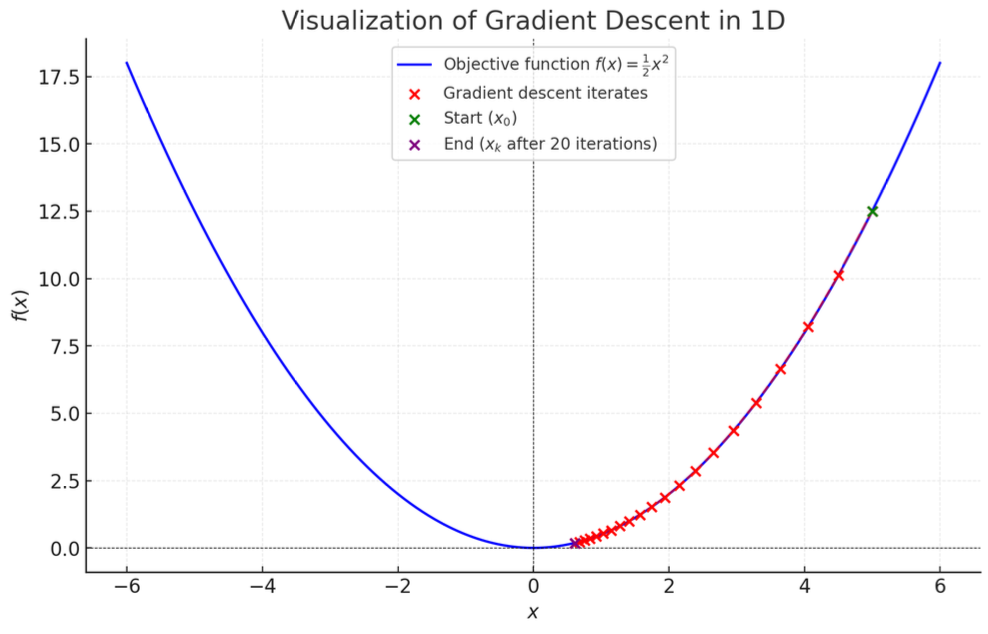
结论:
该示例验证了梯度下降在凸函数上的全局收敛性。步长 η=0.1 满足 0<η<1,确保参数序列单调收敛到最优解 x∗=0。
梯度下降基础分析(Vanilla Analysis)
目标:估计误差上界 f(xt)−f(x∗)
定义梯度 gt:=∇f(xt),由梯度下降更新规则 xt+1=xt−ηgt 可得:
gt=ηxt−xt+1
关键等式推导
-
构造内积项:
gt⊤(xt−x∗)=η1(xt−xt+1)⊤(xt−x∗)
-
应用向量恒等式(2v⊤w=∥v∥2+∥w∥2−∥v−w∥2):
gt⊤(xt−x∗)=2η1(∥xt−xt+1∥2+∥xt−x∗∥2−∥xt+1−x∗∥2)=2η∥gt∥2+2η1(∥xt−x∗∥2−∥xt+1−x∗∥2)
说明:
- 第一项 2η∥gt∥2 控制梯度模长;
- 第二项 2η1(∥xt−x∗∥2−∥xt+1−x∗∥2) 表示参数空间距离变化。
-
对 T 步求和:
t=0∑T−1gt⊤(xt−x∗)=2ηt=0∑T−1∥gt∥2+2η1(∥x0−x∗∥2−∥xT−x∗∥2)
结合凸函数一阶条件
由凸性:f(x∗)≥f(xt)+gt⊤(x∗−xt),可得单步误差上界:
f(xt)−f(x∗)≤gt⊤(xt−x∗)
代入求和式得累积误差界:
t=0∑T−1[f(xt)−f(x∗)]≤2ηt=0∑T−1∥gt∥2+2η1(∥x0−x∗∥2−∥xT−x∗∥2)
核心结论:
- 累积误差由梯度范数之和 ∑∥gt∥2 和初始距离 ∥x0−x∗∥2 控制;
- 步长 η 的平衡作用:
- 过大:梯度项 2η∑∥gt∥2 主导,可能发散;
- 过小:距离项 2η1∥x0−x∗∥2 主导,收敛缓慢。
Lipschitz 凸函数的梯度下降收敛性分析
假设f的所有梯度的范数有界。
等价证明
设函数 f:Rd→R 为凸函数,以下两个性质等价:
-
梯度有界(Bounded Gradient):存在 M>0,使得 ∥∇f(x)∥≤M, ∀x。
-
Lipschitz 连续:存在 L>0,使得 ∥f(y)−f(x)∥≤L∥y−x∥, ∀x,y。
证明过程整理
(⇒) 梯度有界 ⇒ Lipschitz 连续
假设 ∥∇f(x)∥≤M,由微积分基本定理:
f(y)−f(x)=∫01∇f(x+t(y−x))⊤(y−x)dt
取范数并应用 Cauchy-Schwarz 不等式:
∥f(y)−f(x)∥≤∫01∥∇f(x+t(y−x))∥⋅∥y−x∥dt
代入梯度有界条件:
∥f(y)−f(x)∥≤∫01M∥y−x∥dt=M∥y−x∥
即 f 是 M-Lipschitz 连续。
解释:梯度范数有界保证了函数值变化率受控,从而函数整体变化受限于输入变化。
(⇐) Lipschitz 连续 ⇒ 梯度有界
假设 ∥f(y)−f(x)∥≤L∥y−x∥,且 f 为凸函数。需证 ∥∇f(x)∥≤L。
-
若∇f(x)=0:结论显然成立。
-
否则:取 y=x+∇f(x)。
由凸函数的一阶条件:
f(y)≥f(x)+∇f(x)⊤(y−x)
代入 y−x=∇f(x):
f(y)−f(x)≥∇f(x)⊤∇f(x)=∥∇f(x)∥2(∗)
由 Lipschitz 连续性:
f(y)−f(x)≤L∥y−x∥=L∥∇f(x)∥(∗∗)
结合 (∗) 和 (∗∗):
∥∇f(x)∥2≤L∥∇f(x)∥
即 ∥∇f(x)∥≤L。
解释:Lipschitz 连续性限制了函数值的线性增长,迫使梯度范数有界。凸函数的一阶条件将梯度范数与函数值变化关联,完成等价性闭环。
关键公式注释
-
微积分基本定理的应用:
f(y)−f(x)=∫01∇f(x+t(y−x))⊤(y−x)dt
- 意义:将函数值差表示为梯度沿路径 x→y 的积分。
-
Cauchy-Schwarz 不等式:
∇f(z)⊤(y−x)≤∥∇f(z)∥⋅∥y−x∥
-
凸函数一阶条件:
f(y)≥f(x)+∇f(x)⊤(y−x)
- 作用:建立梯度与函数值变化的单向关系(梯度指向函数值增长方向)。
附:P47 示例
对 f(x)=∣x∣:
- 在 x>0 时,gk=1,梯度下降可能越过最优解 x∗=0。
- 在 x=0 时,次梯度 gk∈[−1,1],导致振荡。
说明非光滑函数需专门优化方法(如次梯度法)。
定理设定
设 f:Rd→R 为凸可微函数,且满足:
-
∥x0−x∗∥≤R(初始点与最优解距离有界)
-
∥∇f(x)∥≤B, ∀x(梯度模长有界,等价于 f 是 B-Lipschitz)
收敛证明
-
基础不等式(由 Vanilla Analysis):
t=0∑T−1[f(xt)−f(x∗)]≤2ηt=0∑T−1∥gt∥2+2η1∥x0−x∗∥2
-
代入有界条件:
t=0∑T−1[f(xt)−f(x∗)]≤2ηB2T+2ηR2
-
优化步长 η:定义辅助函数:
h(η)=2ηB2T+2ηR2
- 求导得最优步长:
h′(η)=2B2T−2η2R2=0 ⇒ η∗=BTR
- 代入得最小上界:
h(η∗)=BTR⋅2B2T+2⋅BTRR2=RBT
-
平均误差界:
T1t=0∑T−1[f(xt)−f(x∗)]≤TRB
收敛速率与迭代次数
注:Lipschitz 条件排除了梯度无界的函数(如 f(x)=x2),此类函数需用平滑性分析。
实践建议(R, B 未知时)
-
固定小步长:初始尝试 η=0.01
-
动态调整:
- 若振荡/发散 → 减小 η
- 或采用衰减步长 ηt=t+1η0
-
自适应方法:使用 Adam 等自适应优化器
平滑函数 (Smooth Functions)
定义
设函数 f:dom(f)→R 可微,定义域子集 X⊆dom(f),参数 L>0。若对所有 x,y∈X 满足:
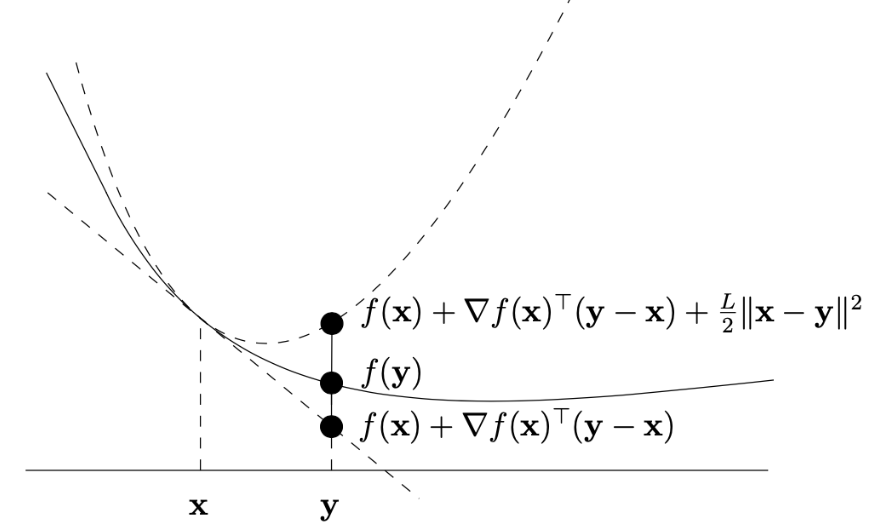
f(y)≤f(x)+∇f(x)⊤(y−x)+2L∥x−y∥2
则称 f 在 X 上是平滑的(参数为 L)。
直观理解:
- 函数“弯曲程度不大”,其值增长不超过一个二次函数(类似抛物面)。
- L 量化了梯度变化的最大速率(梯度变化越快,L 越大)。
几何意义
平滑性表明:在任意点 x 附近,函数 f 可被一个二次函数上界控制(如图形为抛物面)。
示例:
二次函数(如 f(x)=x2)是平滑的。
保持平滑性的运算
以下运算在指定条件下保持函数的平滑性:
引理 1
(i) 设 f1,…,fm 是平滑函数,参数分别为 L1,…,Lm,权重 λ1,…,λm∈R+。则线性组合 f:=∑i=1mλifi 是平滑的,参数为 ∑i=1mλiLi。
(ii) 设 f 是平滑函数(参数 L),g:Rm→Rd 是仿射函数(即 g(x)=Ax+b,其中 A∈Rd×m, b∈Rd)。则复合函数 f∘g(映射 x↦f(Ax+b))是平滑的,参数为 L∥A∥2。
其中 ∥A∥2 是矩阵 A 的谱范数(即最大奇异值)。
凸函数 vs. 平滑函数:性质与优化特性
基本概念对比
| 性质 |
数学定义 |
几何意义 |
优化意义 |
| 凸性 |
f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y) |
函数图像始终在弦下方 |
保证全局最优性 |
| Lipschitz连续性 |
∣∇f(x)∣≤B |
梯度有界,函数变化率受限 |
控制梯度下降的稳定性 |
| 平滑性 |
∣∇f(x)−∇f(y)∣≤L∣x−y∣ |
梯度变化平缓,曲率有界 |
实现更快的收敛速率 |
关键等价关系
引理 2:平滑性的等价刻画
对于凸可微函数 f:Rd→R,以下两个陈述等价:
-
f 是 L-平滑的:f(y)≤f(x)+∇f(x)⊤(y−x)+2L∥x−y∥2
-
梯度是 L-Lipschitz 连续的:∥∇f(x)−∇f(y)∥≤L∥x−y∥
重要性:这建立了函数平滑性与梯度Lipschitz连续性之间的等价关系,为分析优化算法提供了理论基础。
平滑函数的梯度下降分析
引理 3:充分下降性
对于 L-平滑函数,采用步长 η=L1 的梯度下降满足:
f(xt+1)≤f(xt)−2L1∥∇f(xt)∥2
证明:
f(xt+1)≤f(xt)+∇f(xt)⊤(xt+1−xt)+2L∥xt+1−xt∥2=f(xt)−L1∥∇f(xt)∥2+2L1∥∇f(xt)∥2=f(xt)−2L1∥∇f(xt)∥2
意义:每次迭代都保证函数值下降,且下降量由梯度范数控制。
定理 2:收敛速率
对于 L-平滑凸函数,采用 η=L1 的梯度下降满足:
f(xT)−f(x∗)≤2TL∥x0−x∗∥2
证明思路:
-
利用基础分析不等式
-
应用充分下降引理 bound 梯度项
-
通过 telescoping sum 得到最终界
实际应用与比较
收敛速率比较
| 函数类型 |
收敛速率 |
迭代复杂度 (ε-精度) |
| Lipschitz 凸函数 |
O(1/T) |
O(1/ε2) |
| 平滑凸函数 |
O(1/T) |
O(1/ε) |
优势:平滑性使收敛速率从次线性提升到线性,显著提高优化效率。
实践建议:未知 L 的情况
-
初始猜测:设 L=R22ε(如正确,一次迭代可达精度)
-
验证条件:检查 f(xt+1)≤f(xt)−2L1∥∇f(xt)∥2
-
加倍策略:如条件不满足,加倍 L 并重试
-
总复杂度:最多 O(ε4R2L) 次迭代可达精度 ε
实际意义:即使不知道平滑参数,也能通过自适应调整实现高效优化。
次梯度(Subgradient)
次梯度 (Subgradient) 定义
对于凸函数 f:Rd→R,在点 x 的次梯度是任意满足以下条件的向量 g∈Rd:
f(y)≥f(x)+g⊤(y−x),∀y
重要性质:
- 在定义域内点,次梯度总是存在
- 如果 f 在 x 处可微,则次梯度唯一且等于梯度 ∇f(x)
次梯度计算示例
示例 1: 绝对值函数 f(x)=∣x∣
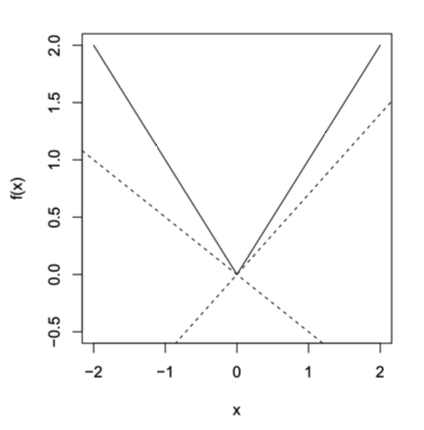
-
当 x=0: 唯一次梯度 g=sign(x)
-
当 x=0: 次梯度为 [−1,1] 区间内任意值
示例 2: L2 范数 f(x)=∥x∥2
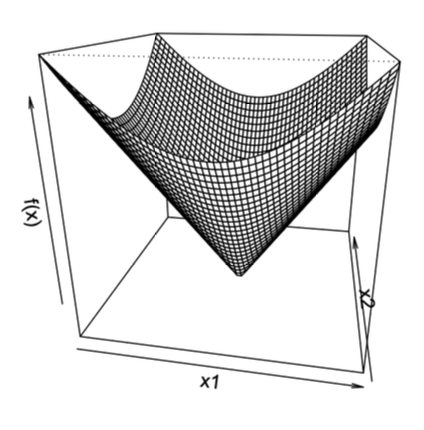
-
当 x=0: 唯一次梯度 g=∥x∥2x
-
当 x=0: 次梯度为闭单位球内任意向量 {z∈Rd:∥z∥2≤1}
示例 3: L1 范数 f(x)=∥x∥1=∑i=1d∣xi∣
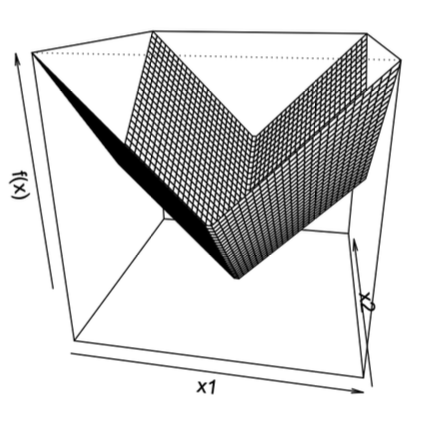
-
当 xi=0: 第 i 个分量 gi=sign(xi)
-
当 xi=0: 第 i 个分量 gi 为 [−1,1] 区间内任意值
示例 4: 集合示性函数 (Indicator Function)
对于凸集 X⊂Rd,示性函数定义为:
1X(x)={0+∞if x∈Xif x∈/X
法锥 (Normal Cone)
定义:给定凸集 X⊆Rd 和点 x∈X,法锥是所有从 x 点向外指向的向量集合:
NX(x)={g∈Rd∣g⊤x≥g⊤y, ∀y∈X}
几何解释:法锥包含的是在点 x 处"支撑"凸集 X 的所有超平面的法向量。这些向量指向集合外部,与集合在该点处的所有可能方向都成直角或钝角。
次微分 (Subdifferential)
定义:凸函数 f:Rd→R 在点 x 的次微分是所有次梯度组成的集合:
∂f(x)={g∈Rd∣f(y)≥f(x)+g⊤(y−x), ∀y∈Rd}
性质:
-
∂f(x) 是闭凸集
-
如果 f 在 x 处可微,则 ∂f(x)={∇f(x)}
-
如果 ∂f(x)={g}(单点集),则 f 在 x 处可微且 ∇f(x)=g
最优性条件
无约束优化
对于任意凸函数 f:Rd→R:
f(x∗)=xminf(x)⟺0∈∂f(x∗)
解释:x∗ 是最小点当且仅当零向量是 f 在 x∗ 处的一个次梯度。
约束优化
考虑约束优化问题:
xminf(x)subject tox∈X
重新表述:引入示性函数 1X(x),将问题等价写为:
xmin{f(x)+1X(x)}
最优性条件:x∗∈X 是最优解当且仅当:
0∈∂(f(x∗)+1X(x∗))=∇f(x∗)+NX(x∗)
这等价于:
−∇f(x∗)∈NX(x∗)
根据法锥定义,上式等价于:
∇f(x∗)⊤(y−x∗)≥0,∀y∈X
几何解释:在最优解 x∗ 处,目标函数的梯度指向可行集内部的相反方向,或者说,梯度与从 x∗ 到可行集内任意点的方向成钝角。
次梯度方法 (Subgradient Method)
基本概念
对于凸函数 f:Rd→R(不一定可微),次梯度方法模仿梯度下降,但用次梯度代替梯度:
xk+1=xk−ηk+1gk
⚠️ 注意:次梯度方法不一定是下降方法。例如 f(x)=∣x∣ 时,非光滑性会导致振荡。
收敛性定理
定理 3:假设 f 是凸函数且 L-Lipschitz(即 ∣f(x)−f(y)∣≤L∥x−y∥)。
-
固定步长 ηk=η(对所有 k):
k→∞limf(xbest(k))≤f∗+2L2η
-
递减步长(满足 ∑k=1∞ηk2<∞ 且 ∑k=1∞ηk=∞):
k→∞limf(xbest(k))≤f∗
其中:
- f(xbest(k))=mini=0,…,kf(xi) 是截至第 k 步的最优值
- f∗=f(x∗) 是真实最小值
证明关键步骤
基于次梯度定义,可推导出基本不等式:
∥xk−x∗∥2≤∥xk−1−x∗∥2−2ηk(f(xk−1)−f∗)+ηk2∥gk−1∥2
迭代该不等式并整理(令 R=∥x0−x∗∥),得到:
0≤R2−2i=1∑kηi(f(xi−1)−f∗)+L2i=1∑kηi2
引入 f(xbest(k)) 后,可得基本不等式:
f(xbest(k))−f∗≤2∑i=1kηiR2+L2∑i=1kηi2
不同步长策略的收敛结果均可由此推导。
固定步长下的收敛率
若固定步长为 η,则有:
f(xbest(k))−f∗≤2kηR2+2L2η
为达到精度 f(xbest(k))−f∗≤ε,可令两项各 ≤ε/2,解得:
因此,次梯度方法的收敛率为 O(ε21)。
📉 对比:梯度下降法在光滑凸函数上的收敛率为 O(ε1),表明次梯度方法收敛更慢。
算法收敛性总结
| 函数性质 |
算法 |
收敛界 |
迭代次数 |
| 凸、L-Lipschitz |
次梯度 |
f(xbest(T))−f∗≤TLR |
O(ε2R2L2) |
| 凸、L-光滑 |
梯度下降 |
f(xbest(T))−f∗≤2TR2L |
O(εR2L) |
| 凸、L-Lipschitz |
梯度下降 |
f(xbest(T))−f∗≤TRL |
O(ε2R2L2) |
其中:
- T:时间范围/迭代次数
- R=∥x0−x∗∥:初始点与最优点的距离
- xbest(T)=argmini=0,1,…,Tf(xi):前 T 次迭代中的最优点
总结
展开
凸函数定义
函数 f:Rd→R 是凸函数当且仅当:
-
定义域 dom(f) 是凸集;
-
对所有 x,y∈dom(f) 和 λ∈[0,1],满足:
f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)
几何意义:函数图像上任意两点间的线段位于图像上方。
一阶凸性刻画
若 f 可微,则凸性等价于:
f(y)≥f(x)+∇f(x)⊤(y−x),∀x,y∈dom(f)
几何意义:函数图像始终在其切超平面的上方。
可微函数
-
定义:f 在 x0 可微当存在梯度 ∇f(x0) 使得:
f(x0+h)≈f(x0)+∇f(x0)⊤h
其中 h 为微小扰动。
-
全局可微:若在定义域内每点可微,则称 f 可微,其图像在各点有非垂直切超平面。
凸优化问题
形式:
x∈Rdminf(x)
其中 f 是凸可微函数,Rd 是凸集。全局最小值点记为 x∗=argminf(x)(可能有多个)。
梯度下降法 (Gradient Descent)
核心思想
利用负梯度方向更新参数(梯度 ∇f(x) 指向函数值增长最快的方向):
xk+1=xk−ηk∇f(xk)
-
ηk:步长(学习率)
-
xk:当前参数
收敛性分析
Lipschitz 凸函数(梯度有界)
假设:∥∇f(x)∥≤B,∥x0−x∗∥≤R
步长选择:η=BTR
收敛速率:
T1t=0∑T−1[f(xt)−f(x∗)]≤TRB
优势:收敛速率与维度 d 无关。
实践建议:若 B,R 未知,可尝试小步长(如 η=0.01)或自适应步长(如 Adam)。
平滑凸函数(梯度 Lipschitz 连续)
定义:f 是 L-平滑的当满足:
f(y)≤f(x)+∇f(x)⊤(y−x)+2L∥x−y∥2
等价于 ∥∇f(x)−∇f(y)∥≤L∥x−y∥。
步长选择:η=L1
收敛速率:
f(xT)−f(x∗)≤2TL∥x0−x∗∥2
对比:平滑函数收敛速率 O(1/ε) 优于 Lipschitz 函数的 O(1/ε2)。
实践建议:若 L 未知,可通过加倍试探并验证充分下降条件 f(xt+1)≤f(xt)−2L1∥∇f(xt)∥2。
次梯度方法 (Subgradient Method)
次梯度定义
对凸函数 f,在 x 的次梯度 g∈∂f(x) 满足:
f(y)≥f(x)+g⊤(y−x),∀y
关键性质:
- 可微时 ∂f(x)={∇f(x)};
- 最优性条件:x∗ 是最小点当且仅当 0∈∂f(x∗)。
更新规则
xk+1=xk−ηkgk,gk∈∂f(xk)
注意:次梯度法非下降方法(例如 f(x)=∣x∣ 可能振荡)。
收敛性
假设:f 是 L-Lipschitz 凸函数
-
固定步长 η:极限误差 ≤f∗+L2η/2
-
衰减步长(∑ηk=∞, ∑ηk2<∞):渐近收敛到 f∗
收敛速率:
f(xbest(k))−f∗≤2∑i=1kηiR2+L2∑i=1kηi2
其中 R=∥x0−x∗∥,fbest(k)=mini=0,…,kf(xi)。





