#sdsc6015
English / 中文
回顾
点击展开
凸优化问题的一般形式为:
x∈Rdminf(x)
其中 f 是凸函数,Rd 是凸集,x∗ 是其最小化点:
x∗=argx∈Rdminf(x)
梯度下降(Gradient Descent, GD)的更新规则为:
xk+1=xk−ηk+1∇f(xk)
定义:
若函数 f:dom(f)→R 可微,且存在 L>0,使得对所有 x,y∈X⊆dom(f) 有:
f(y)≤f(x)+∇f(x)⊤(y−x)+2L∥x−y∥2
则称 f 是**L-平滑的**。
💡 平滑性意味着函数的梯度变化不会太快,上界由 L 控制。
定义:
对于凸函数 f:Rd→R,在点 x 处的次梯度 g 满足:
f(y)≥f(x)+g⊤(y−x),∀y
所有次梯度的集合称为次微分:
∂f(x)={g∈Rd∣g 是 f 在 x 处的次梯度}
🔍 对于可微凸函数,次微分就是梯度;对于不可微函数(如 ∣x∣),次梯度可能不唯一。
次梯度方法:
更新规则为:
xk+1=xk−ηk+1gk,gk∈∂f(xk)
| 函数性质 |
算法 |
收敛界 |
迭代次数(达到误差 ε) |
| Convex, L-Lipschitz |
GD |
f(xbest(T))−f(x∗)≤TRL |
O(ε2R2L2) |
| Convex, L-Smooth |
GD |
f(xbest(T))−f(x∗)≤2TR2L |
O(2εR2L) |
| μ-SC, L-Smooth |
GD |
f(xbest(T))−f(x∗)≤2L(1−Lμ)TR2 |
O(μLln2εR2L) |
| Convex, L-Lipschitz |
Subgradient |
f(xbest(T))−f(x∗)≤TLR |
O(ε2R2L2) |
| μ-SC, ∣g∣≤B |
Subgradient |
f(xbest(T))−f(x∗)≤μ(T+1)2B2 |
O(με2B2) |
其中:
-
R=∥x0−x∗∥
-
xbest(T)=argmini=0,…,Tf(xi)
强凸函数(Strongly Convex Functions)
定义
一个函数 f:dom(f)→R 被称为强凸函数(strongly convex),如果存在参数 μ>0,使得对于所有 x,y∈dom(f)(其中 dom(f) 是凸集),都有:
f(y)≥f(x)+∇f(x)⊤(y−x)+2μ∥y−x∥2

这里,∇f(x) 是 f 在点 x 处的梯度(如果 f 可微)。
对于不可微函数,次梯度版本的定义为:对于所有 g∈∂f(x)(次微分),有:
f(y)≥f(x)+g⊤(y−x)+2μ∥y−x∥2
💡 直观解释:强凸函数在任意点 x 处,其函数值都高于一个“加强的”线性近似(即加上一个二次项 2μ∥y−x∥2)。这确保了函数具有更强的曲率,从而优化时收敛更快。
关键性质
(1)强凸性蕴含严格凸性
如果 f 是 μ-强凸的,那么它也是严格凸的。这意味着对于所有 x=y 和 λ∈(0,1),有:
f(λx+(1−λ)y)<λf(x)+(1−λ)f(y)
证明概要(来自补充笔记 p15):
假设 x=y,令 z=λx+(1−λ)y。由强凸性:
f(x)f(y)>f(z)+∇f(z)⊤(x−z)>f(z)+∇f(z)⊤(y−z)
将这两个不等式加权平均(权重为 λ 和 1−λ),梯度项抵消,得到:
λf(x)+(1−λ)f(y)>f(z)
从而证得严格凸性。
(2)存在唯一全局最小值
强凸函数有且仅有一个全局最小值点 x∗。
证明概要(来自补充笔记 p15):
假设 x∗ 是最小点,则 ∇f(x∗)=0(可微情况)或 0∈∂f(x∗)(不可微情况)。由强凸性:
f(y)≥f(x∗)+2μ∥y−x∗∥2
当 y=x∗ 时,2μ∥y−x∗∥2>0,因此 f(y)>f(x∗),即 x∗ 是唯一的。
例子
强凸函数的一个典型例子是 f(x)=e∣x∣,它对于某些参数 μ 是强凸的。具体地,当 μ=1 时,该函数满足强凸定义。
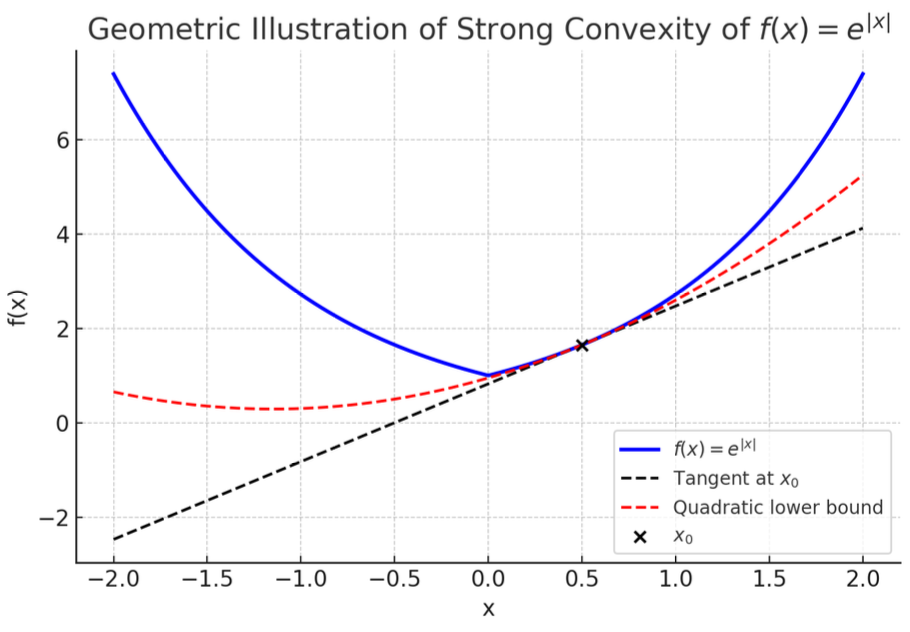
在优化中的应用
强凸性显著改善了优化算法的收敛速率。以下分两种情况讨论:
(1)梯度下降(Gradient Descent)用于平滑且强凸的函数
如果 f 是 L-平滑且 μ-强凸的(即可微),则选择步长 η=L1,梯度下降的迭代点满足:
∥xt+1−x∗∥2≤(1−Lμ)∥xt−x∗∥2
误差按指数衰减:
f(xT)−f(x∗)≤2L(1−Lμ)T∥x0−x∗∥2
证明:
从梯度下降更新:xt+1=xt−η∇f(xt)。
考虑距离变化:
∥xt+1−x∗∥2=∥xt−η∇f(xt)−x∗∥2=∥xt−x∗∥2−2η∇f(xt)⊤(xt−x∗)+η2∥∇f(xt)∥2
由强凸性:
∇f(xt)⊤(xt−x∗)≥f(xt)−f(x∗)+2μ∥xt−x∗∥2
代入:
∥xt+1−x∗∥2≤∥xt−x∗∥2−2η(f(xt)−f(x∗)+2μ∥xt−x∗∥2)+η2∥∇f(xt)∥2
整理:
∥xt+1−x∗∥2≤(1−μη)∥xt−x∗∥2−2η(f(xt)−f(x∗))+η2∥∇f(xt)∥2
现在取 η=1/L。由平滑性,有充分下降引理:
f(xt+1)≤f(xt)−2L1∥∇f(xt)∥2
因此,−2L1∥∇f(xt)∥2≤f(xt+1)−f(xt),但这里我们需要 bound η2∥∇f(xt)∥2。
实际上,从平滑性,有:
f(x∗)≤f(xt)−2L1∥∇f(xt)∥2
所以 ∥∇f(xt)∥2≤2L(f(xt)−f(x∗))。
代入:
η2∥∇f(xt)∥2=L21∥∇f(xt)∥2≤L2(f(xt)−f(x∗))
于是:
∥xt+1−x∗∥2≤(1−μη)∥xt−x∗∥2−2η(f(xt)−f(x∗))+L2(f(xt)−f(x∗))
由于 η=1/L,−2η+L2=0,所以:
∥xt+1−x∗∥2≤(1−Lμ)∥xt−x∗∥2
这证明了第一部分。
对于第二部分,由平滑性:
f(xT)−f(x∗)≤2L∥xT−x∗∥2≤2L(1−Lμ)T∥x0−x∗∥2
证毕。
迭代次数需求:要达到误差 ε,需要迭代次数为:
T≥μLln(2εR2L),其中 R=∥x0−x∗∥
这比非强凸情况(如平滑凸函数的 O(1/ε) 速率)快得多,因为误差以 O(e−T) 衰减。
(2)次梯度方法(Subgradient Method)用于强凸函数
如果 f 是 μ-强凸的(可能不可微),且次梯度范数有界(即 ∥gt∥≤B 对于所有 gt∈∂f(xt)),则采用递减步长:
ηt=μ(t+1)2
并计算加权平均点:
xˉT=T(T+1)2t=1∑Tt⋅xt
则收敛速率为:
f(xˉT)−f(x∗)≤μ(T+1)2B2
证明:
从次梯度更新:xt+1=xt−ηtgt,其中 gt∈∂f(xt)。
考虑距离变化:
∥xt+1−x∗∥2=∥xt−ηtgt−x∗∥2=∥xt−x∗∥2−2ηtgt⊤(xt−x∗)+ηt2∥gt∥2
由强凸性:
gt⊤(xt−x∗)≥f(xt)−f(x∗)+2μ∥xt−x∗∥2
代入:
∥xt+1−x∗∥2≤∥xt−x∗∥2−2ηt(f(xt)−f(x∗)+2μ∥xt−x∗∥2)+ηt2∥gt∥2
整理:
∥xt+1−x∗∥2≤(1−μηt)∥xt−x∗∥2−2ηt(f(xt)−f(x∗))+ηt2B2
现在移项:
2ηt(f(xt)−f(x∗))≤(1−μηt)∥xt−x∗∥2−∥xt+1−x∗∥2+ηt2B2
代入步长 ηt=μ(t+1)2,则 1−μηt=1−t+12=t+1t−1。
两边乘以 t(为了 telescoping):
2tηt(f(xt)−f(x∗))≤t(1−μηt)∥xt−x∗∥2−t∥xt+1−x∗∥2+tηt2B2
注意 t(1−μηt)=t⋅t+1t−1=t+1t(t−1),且 tηt2=t⋅μ2(t+1)24=μ2(t+1)24t。
但更直接的是,观察:
t(1−μηt)=t+1t(t−1),而(t+1)∥xt+1−x∗∥2可能出现
实际上,从原不等式:
2ηt(f(xt)−f(x∗))≤2ηt2B2+2ηt1(∥xt−x∗∥2−∥xt+1−x∗∥2)−2μ∥xt−x∗∥2
但课程材料中采用了另一种方式。
根据课程材料证明:
从不等式:
f(xt)−f(x∗)≤2B2ηt+2ηt−1−μ∥xt−x∗∥2−2ηt−1∥xt+1−x∗∥2
代入 ηt=μ(t+1)2,则 ηt−1=2μ(t+1)。
所以:
f(xt)−f(x∗)≤2B2⋅μ(t+1)2+21(2μ(t+1)−μ)∥xt−x∗∥2−21⋅2μ(t+1)∥xt+1−x∗∥2
简化:
f(xt)−f(x∗)≤μ(t+1)B2+4μ((t+1)−2)∥xt−x∗∥2−4μ(t+1)∥xt+1−x∗∥2
即:
f(xt)−f(x∗)≤μ(t+1)B2+4μ(t−1)∥xt−x∗∥2−4μ(t+1)∥xt+1−x∗∥2
两边乘以 t:
t(f(xt)−f(x∗))≤μ(t+1)tB2+4μ(t(t−1)∥xt−x∗∥2−t(t+1)∥xt+1−x∗∥2)
对 t=1 到 T 求和:
t=1∑Tt(f(xt)−f(x∗))≤t=1∑Tμ(t+1)tB2+4μ(t=1∑T[t(t−1)∥xt−x∗∥2−t(t+1)∥xt+1−x∗∥2])
右边第二项是 telescoping 和:
t=1∑T[t(t−1)∥xt−x∗∥2−t(t+1)∥xt+1−x∗∥2]=−T(T+1)∥xT+1−x∗∥2≤0
因为 t=1 时 1⋅0⋅∥x1−x∗∥2=0,之后项抵消。
所以:
t=1∑Tt(f(xt)−f(x∗))≤t=1∑Tμ(t+1)tB2≤μTB2
由凸性,加权平均满足:
f(T(T+1)2t=1∑Ttxt)≤T(T+1)2t=1∑Ttf(xt)
所以:
f(T(T+1)2t=1∑Ttxt)−f(x∗)≤T(T+1)2t=1∑Tt(f(xt)−f(x∗))≤T(T+1)2⋅μTB2=μ(T+1)2B2
证毕。
迭代次数需求:要达到误差 ε,需要迭代次数为 O(μεB2)。
🔍 *注意:加权平均有助于稳定收敛,避免次梯度振荡。但次梯度方法不是下降方法,因此平均化是必要的。
投影梯度下降 (Projected Gradient Descent)
约束优化问题
x∈Xminf(x)
其中 X⊆Rd 是闭凸集。
投影算子
投影 onto X 定义为:
ΠX(y)=argx∈Xmin∥x−y∥

更新规则
yt+1xt+1=xt−ηt∇f(xt)=ΠX(yt+1)
投影性质
-
(x−ΠX(y))⊤(y−ΠX(y))≤0 for all x∈X
-
∥x−ΠX(y)∥2+∥y−ΠX(y)∥2≤∥x−y∥2 for all x∈X
证明:
-
由于 ΠX(y) 最小化 ∥x−y∥2 over X,由最优性条件,对任意 x∈X,有:
(ΠX(y)−y)⊤(x−ΠX(y))≥0
即 (x−ΠX(y))⊤(y−ΠX(y))≤0。
-
从1,有:
∥x−y∥2=∥x−ΠX(y)+ΠX(y)−y∥2=∥x−ΠX(y)∥2+∥ΠX(y)−y∥2+2(x−ΠX(y))⊤(ΠX(y)−y)
由于 (x−ΠX(y))⊤(ΠX(y)−y)≥0,所以:
∥x−y∥2≥∥x−ΠX(y)∥2+∥ΠX(y)−y∥2
即性质2。
收敛速率
投影梯度下降的收敛速率与无约束情况相同,取决于函数性质:
-
如果 f 是凸且 L-Lipschitz over X,则误差 O(1/T),迭代次数 O(1/ε2)。
-
如果 f 是凸且 L-平滑 over X,则误差 O(1/T),迭代次数 O(1/ε)。
-
如果 f 是 μ-强凸且 L-平滑 over X,则误差 O(e−cT),迭代次数 O(log(1/ε))。
证明草图:与无约束证明类似,但使用投影性质 bound ∥xt+1−x∗∥2。例如,对于 Lipschitz 情况:
从更新:
yt+1=xt−η∇f(xt)
由投影性质2,有:
∥xt+1−x∗∥2≤∥yt+1−x∗∥2−∥yt+1−xt+1∥2≤∥yt+1−x∗∥2
然后与无约束类似分析。
总结表格
| 函数性质 |
算法 |
收敛速率 |
迭代次数 |
| 凸、L-Lipschitz |
梯度下降 |
f(xbest(T))−f(x∗)≤TRL |
O(1/ε2) |
| 凸、L-平滑 |
梯度下降 |
f(xbest(T))−f(x∗)≤2TR2L |
O(1/ε) |
| 凸、L-Lipschitz |
次梯度法 |
f(xbest(T))−f(x∗)≤TLR |
O(1/ε2) |
| μ-强凸、L-平滑 |
梯度下降 |
f(xbest(T))−f(x∗)≤2RL(1−Lμ)T |
O(log(1/ε)) |
| μ-强凸、∣g∣≤B |
次梯度法 |
f(xbest(T))−f(x∗)≤μ(T+1)2B2 |
O(1/ε) |
其中 R=∥x0−x∗∥。
注意:实际应用中,步长选择对收敛至关重要。对于未知参数的情况,可能需要自适应步长策略。
补充说明
-
强凸与 Lipschitz 的冲突:
非光滑函数不能同时是 Lipschitz 和强凸的(例如 f(x)=x 在 x=0 附近无界)。
-
次梯度范数与 Lipschitz 的关系:
- Lipschitz 连续性 ⇒ 次梯度有界
- 次梯度有界 ⇒ Lipschitz 连续
-
最优性:
一阶方法(梯度/次梯度)的收敛速率在一般情况下是最优的,无法进一步改进。
⚙️




