#sdsc6015
English / 中文
投影梯度下降 (Projected Gradient Descent)
投影梯度下降是处理约束优化问题的算法,通过梯度步后投影回可行集来确保约束满足。
约束优化问题定义
约束优化问题形式化定义为:
minf(x)subject tox∈X
其中:
-
f:Rd→R 是目标函数
-
X⊆Rd 是一个闭凸集(closed convex set)
-
x∈Rd 是优化变量
几何意义:在满足约束 x∈X 的前提下,寻找使 f(x) 最小的点。
算法描述
投影梯度下降迭代步骤:
For t=0,1,2,… with stepsize ηt>0:yt+1=xt−ηt∇f(xt)xt+1=ΠX(yt+1)
其中投影算子定义为:
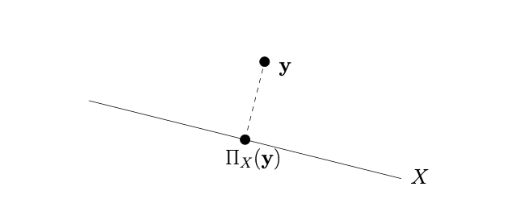
ΠX(y):=x∈Xargmin∥x−y∥
数学符号意义:
收敛速率分析
收敛速率与无约束梯度下降相同,但每一步需要投影操作:
-
Lipschitz 凸函数(参数 G):O(1/ε2) 步
-
光滑凸函数(参数 L):O(1/ε) 步
-
光滑强凸函数(参数 μ,L):O(log(1/ε)) 步
计算效率取决于投影操作的难易程度。
光滑函数上的收敛性
光滑性定义:函数 f 在闭凸集 X⊆Rd 上称为光滑(参数 L),如果:
∥∇f(x)−∇f(y)∥≤L∥x−y∥,∀x,y∈X
引理1(充分下降):
设 f:Rd→R 可微且在闭凸集 X⊆Rd 上光滑(参数 L)。选择步长 η=1/L,投影梯度下降满足:
f(xt+1)≤f(xt)−2L1∥∇f(xt)∥2+2L∥yt+1−xt+1∥2
其中 yt+1=xt−η∇f(xt)。
引理1证明:
数学符号在投影中的意义
-
yt+1=xt−η∇f(xt):这是未投影的梯度步,即沿着梯度方向移动一步后的点,但可能不在可行集 X 中。
-
xt+1=ΠX(yt+1):这是投影后的点,通过投影算子 ΠX 将 yt+1 映射到 X 中最近的点,确保迭代点始终满足约束。
-
∥yt+1−xt+1∥2:这是投影误差,衡量未投影点与投影点之间的欧几里得距离平方。这个项在不等式中的作用是“惩罚”投影带来的偏差,因为投影操作可能使点偏离梯度方向。
-
ΠX(y):=argminx∈X∥x−y∥:投影算子,表示将点 y 投影到闭凸集 X 上,找到 X 中离 y 最近的点。
证明
引理1的证明依赖于三个关键要素:函数的光滑性、投影的最优性条件、以及投影算子的几何性质(Fact(ii))。以下是证明步骤的详细解释:
-
利用函数光滑性:由于 f 是 L-光滑的,根据光滑性定义,对于任意点 x 和 y,有:
f(y)≤f(x)+∇f(x)⊤(y−x)+2L∥y−x∥2
应用此性质于 x=xt 和 y=yt+1,并代入 yt+1=xt−η∇f(xt) 和 η=1/L,得到:
f(yt+1)≤f(xt)−2L1∥∇f(xt)∥2
这一步给出了未投影点 yt+1 的函数值上界。
-
投影的最优性条件:由于 xt+1=ΠX(yt+1) 是投影点,对于闭凸集 X,投影算子满足以下最优性条件:对于任意 x∈X,有:
(x−xt+1)⊤(yt+1−xt+1)≤0
特别地,取 x=xt(因为 xt∈X),有:
(xt−xt+1)⊤(yt+1−xt+1)≤0
代入 yt+1=xt−η∇f(xt),经过代数变换,可得:
∇f(xt)⊤(xt+1−xt)≤−η1∥xt−xt+1∥2
这个不等式将梯度内积与投影后的移动距离关联起来。
-
应用光滑性于 xt+1:再次利用光滑性定义,这次应用于 x=xt 和 y=xt+1:
f(xt+1)≤f(xt)+∇f(xt)⊤(xt+1−xt)+2L∥xt+1−xt∥2
将步骤2中的不等式代入,得到:
f(xt+1)≤f(xt)−η1∥xt−xt+1∥2+2L∥xt+1−xt∥2
代入 η=1/L,简化得:
f(xt+1)≤f(xt)−2L∥xt−xt+1∥2
-
利用投影性质(Fact(ii)):附件2中提到的 Fact(ii) 是投影算子的一个几何性质:对于任意 x∈X 和 y∈Rd,有:
∥x−ΠX(y)∥2+∥y−ΠX(y)∥2≤∥x−y∥2
取 x=xt 和 y=yt+1,且 ΠX(yt+1)=xt+1,得到:
∥xt−xt+1∥2+∥yt+1−xt+1∥2
定理1:
设 f:Rd→R 是一个凸且可微的函数。令 X⊆Rd 是一个闭凸集,并假设存在一个最小化器 x∗∈X 使得 f(x∗)=minx∈Xf(x)。进一步,假设 f 在 X 上是光滑的(即梯度是 L-利普希茨连续),参数为 L。选择步长 η=L1,则投影梯度下降算法产生的迭代序列满足以下收敛界:
f(xT)−f(x∗)≤2TL∥x0−x∗∥2
其中 xT 是第 T 次迭代后的点,x0 是初始点。
定理1证明:
符号解释 (Notation Explanation)
-
f:目标函数,从 Rd 映射到 R,凸且可微。
-
X:可行域,一个闭凸集(例如,约束条件定义的区域)。
-
x∗:f 在 X 上的全局最小点,即 x∗=argminx∈Xf(x)。
-
L:光滑常数(Lipschitz 常数),表示梯度的变化上界,即 ∥∇f(x)−∇f(y)∥≤L∥x−y∥ 对所有 x,y∈X 成立。
-
η:步长,在定理中设为 η=L1 以确保收敛。
-
gt:在点 xt 处的梯度,即 gt=∇f(xt)。
-
xt:第 t 次迭代后的点(投影后)。
-
yt+1:未投影的梯度步,计算为 yt+1=xt−ηgt。
-
xt+1:投影后的点,即 xt+1=ΠX(yt+1),其中 ΠX 是到集合 X 的投影算子。
投影算子 ΠX(y) 返回 X 中离 y 最近的点,即 ΠX(y)=argminx∈X∥x−y∥。由于 X 是闭凸集,投影存在且唯一。
证明概述 (Proof Sketch)
证明的核心在于利用函数的光滑性和凸性,以及投影算子的性质,来推导每次迭代的误差界。以下是关键步骤:
-
充分下降条件 (Sufficient Decrease)
由于 f 是 L-光滑的,对于投影梯度下降,有以下的充分下降不等式:
f(xt+1)≤f(xt)−2L1∥gt∥2+2L∥yt+1−xt+1∥2
这个不等式表明,每次迭代后函数值下降的量受梯度大小和投影误差的影响。额外项 2L∥yt+1−xt+1∥2 是由于投影操作引入的。
-
投影算子的性质 (Projection Property)
使用投影算子的一个关键事实(Fact ii):对于任意 x∈X 和 y∈Rd,有
∥x−ΠX(y)∥2+∥y−ΠX(y)∥2≤∥x−y∥2
令 x=x∗(最优解)和 y=yt+1,由于 ΠX(yt+1)=xt+1,我们得到:
∥x∗−xt+1∥2+∥yt+1−xt+1∥2≤∥x∗−yt+1∥2
这个不等式反映了投影的“正交性”,即投影点与原始点的距离关系。
-
结合凸性 (Combining with Convexity)
由 f 的凸性,有:
f(xt)−f(x∗)≤gt⊤(xt−x∗)
这表示函数值差被梯度与点差的内积所控制。
-
代数操作与抵消 (Algebraic Manipulation and Cancellation)
将上述元素结合。首先,从普通梯度下降的分析框架出发,但用 yt+1 替代 xt+1(因为 yt+1 是未投影的步骤)。然后,利用投影性质不等式和充分下降条件,通过代数操作发现额外项 ∥yt+1−xt+1∥2 在求和时抵消。具体地,当步长 η=L1 时,有:
t=0∑T−1(f(xt)−f(x∗))≤2L∥x0−x∗∥2
由于 f(xt) 是递减的(由充分下降保证),最终得到 f(xT)−f(x∗)≤2TL∥x0−x∗∥2.
证明中的关键洞察是:投影操作虽然引入了误差项,但通过投影算子的性质,这些误差在整体分析中相互抵消,从而保持了与无约束梯度下降相同的收敛速率。
几何意义 (Geometric Interpretation)
-
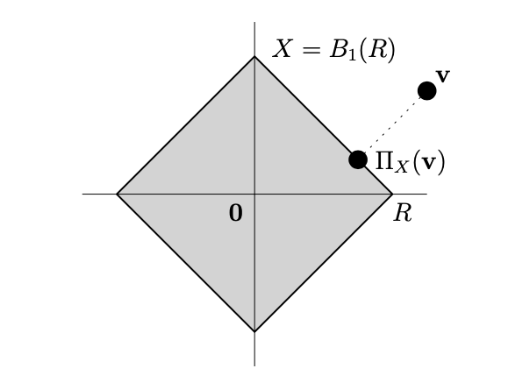
投影的作用:投影梯度下降通过将梯度步 yt+1 投影回可行集 X 来确保迭代点始终满足约束。投影操作可以看作是将点“拉回”到可行域上最近的点。
-
收敛行为:由于函数光滑且凸,梯度方向指向下降方向,但投影可能改变路径。定理表明,即使有投影,收敛速率仍为 O(1/T),与无约束情况相同。这是因为投影误差在长期迭代中平均化,不影响整体趋势。
-
直观理解:想象一个球在光滑凸面上滚动,每次沿梯度方向移动,但被约束在可行区域内。投影确保球不离开区域,而光滑性保证移动不会过度振荡,最终稳定到最低点。
例子 (Example)
虽然文档中没有提供具体例子,但一个典型应用是带约束的线性回归:目标函数 f(x)=∥Ax−b∥2 是光滑凸的,约束集 X 可能是非负象限(x≥0)。投影梯度下降通过迭代更新 x 并投影到 X 上,确保解满足非负性,同时以 O(1/T) 速率收敛。
附注 (Additional Notes)
-
定理假设了函数的光滑性和凸性,在实际中需验证这些条件。
-
步长 η=1/L 是理论上的最优选择,但实践中可能使用自适应步长。
-
收敛率 O(1/T) 是次线性的,对于大规模问题可能较慢,但这是凸优化中的标准结果。
强凸光滑函数上的收敛性
强凸函数定义:函数 f 在集合 X 上是强凸的(参数为 μ>0),如果对于所有 x,y∈X,满足:
f(y)≥f(x)+∇f(x)⊤(y−x)+2μ∥y−x∥2
这意味着函数具有一个下界二次项,确保其曲率有下界,从而加速优化收敛。
强凸函数的性质
引理2证明:
数学符号与意义
定理陈述
如果函数 f 在集合 X 上是 μ-强凸的,那么 f 在 X 上存在唯一的最小化器 x∗。
证明
-
存在性:由于 f 是强凸函数,它也是凸函数,且 X 是闭凸集,因此最小值存在。
-
唯一性(反证法):
- 假设存在两个不同的最小化器 x1∗ 和 x2∗,且 f(x1∗)=f(x2∗)=f∗
- 考虑中点 xm=2x1∗+x2∗
- 由强凸性定义:
f(xm)≤21f(x1∗)+21f(x2∗)−8μ∥x1∗−x2∗∥2
f(xm)≤f∗−8μ∥x1∗−x2∗∥2<f∗
- 这与 f∗ 是最小值的假设矛盾
- 因此最小化器必须唯一
几何意义
强凸函数具有"陡峭的碗状"结构,确保函数只有一个全局最小值点,没有任何平坦区域或多个局部最小值。μ 值越大,函数的"碗"形状越陡峭,优化过程更容易找到唯一解。
投影梯度下降的收敛性(Theorem 2)
定理证明:
数学符号与意义
-
L: 平滑性参数(Lipschitz常数)
-
η=1/L: 最优步长选择
-
xt: 第 t 次迭代后的解
-
yt+1=xt−η∇f(xt): 未投影的梯度步
-
xt+1=ΠX(yt+1): 投影后的解
定理陈述
对于 μ-强凸且 L-平滑的函数 f,采用步长 η=1/L 的投影梯度下降满足:
(i) 平方距离几何递减:
∥xt+1−x∗∥2≤(1−Lμ)∥xt−x∗∥2
(ii) 函数值误差指数收敛:
f(xT)−f(x∗)≤2L(1−Lμ)T∥x0−x∗∥2
证明概要
关键步骤:
-
梯度不等式:
∇f(xt)⊤(xt−x∗)≥f(xt)−f(x∗)+2μ∥xt−x∗∥2
-
投影性质(附件2 P8):
f(xt+1)≤f(xt)−2L1∥∇f(xt)∥2+2L∥yt+1−xt+1∥2
-
距离递归关系:
- 结合投影算子的非扩张性:∥ΠX(y)−ΠX(z)∥≤∥y−z∥
- 利用平滑性:f(y)≤f(x)+∇f(x)⊤(y−x)+2L∥y−x∥2
-
最终推导:
∥xt+1−x∗∥2≤∥yt+1−x∗∥2−∥yt+1−xt+1∥2=∥xt−η∇f(xt)−x∗∥2−∥yt+1−xt+1∥2≤(1−Lμ)∥xt−x∗∥2
几何意义与解释
条件数 κ=L/μ:该定理揭示了收敛速率取决于函数的光滑性 (L) 与强凸性 (μ) 的比值。条件数越小(即函数越强凸或越平滑),收敛越快。
几何解释:
- 强凸性确保函数有明确的"下降方向"
- 平滑性确保梯度变化不会太剧烈,允许使用较大步长
- 投影操作确保解始终保持在可行域 X 内
- 每次迭代都会将当前解指数级地拉向唯一最优解
实际意义:该定理保证了在合理条件下,投影梯度下降能够快速收敛到最优解,且误差随迭代次数指数下降。步长 η=1/L 是最优选择,平衡了收敛速度和稳定性。
投影步的计算例子
近端梯度下降法 (Proximal Gradient Descent)
问题设定
考虑复合优化问题,目标函数由两部分组成:
f(x):=g(x)+h(x)
数学符号意义:
近端梯度下降法适用于求解非光滑、带约束或具有特殊结构的优化问题。
算法思想与更新公式
核心思想:将梯度下降思想推广到复合函数。对于光滑函数g(x),梯度下降步等价于最小化局部二次近似:
xt+1=argzmin{g(xt)+∇g(xt)⊤(z−xt)+2η1∥z−xt∥2}
对于f=g+h,保留对g的二次近似,直接加上h:
xt+1=argzmin{g(xt)+∇g(xt)⊤(z−xt)+2η1∥z−xt∥2+h(z)}
算法迭代公式:
xt+1=proxh,η(xt−η∇g(xt))
近端映射定义:
proxh,η(z)=argxmin{2η1∥x−z∥2+h(x)}
等价形式:
xt+1=xt−ηGh,η(xt)
其中Gh,η(x)=η1(x−proxh,η(x−η∇g(x)))为广义梯度
特例与几何意义
h=0:退化为标准梯度下降
prox0,η(z)=z
h=1X(指示函数):退化为投影梯度下降
-
指示函数:1X(x)={0,∞,x∈Xx∈/X
-
近端映射变为投影:prox1X,η(z)=πX(z)=argminx∈X∥x−z∥
几何意义:近端映射在点z附近寻找使h(x)较小的点,参数η平衡"接近z"和"使h小"两个目标。
收敛性分析
定理3(近端梯度下降收敛性)
设g:Rd→R凸且L-光滑,h凸,且可计算近端映射。选择步长η=1/L,则:
f(xT)−f(x∗)≤2TL∥x∗−x0∥2
收敛速率为O(1/T),与光滑凸函数上的梯度下降相同。
定理3证明思路:
数学符号意义
-
ψ(z)=g(xt)+∇g(xt)⊤(z−xt)+2η1∥z−xt∥2+h(z):局部近似函数
-
xt+1=argminzψ(z):近端梯度步
-
∥y−xt+1∥2:近似误差项,衡量当前点与最优点的距离
证明步骤
-
定义局部近似函数:
ψ(z)=g(xt)+∇g(xt)⊤(z−xt)+2η1∥z−xt∥2+h(z)
由于二次项存在,ψ(z)是强凸函数。
-
利用强凸性:根据xt+1的定义和ψ的强凸性:
ψ(xt+1)≤ψ(y)−2η1∥y−xt+1∥2,∀y
-
转化为f的递减性质:利用g的L-光滑性和凸性,将不等式转化为:
f(xt+1)≤f(y)+2η1∥y−xt∥2−2η1∥y−xt+1∥2,∀y
-
求和与单调性:
- 令y=x∗,对t=0到T−1求和
- 利用函数值单调递减:f(xt+1)≤f(xt)
- 得到最终收敛界
几何直观:近端方法只"看到"光滑部分g,非光滑部分h被近端映射单独处理,不影响收敛速度。
实例:迭代软阈值算法 (ISTA)
Lasso回归问题:
βmin21∥y−Aβ∥22+λ∥β∥1
数学符号意义:
-
A∈Rn×d:特征矩阵
-
y∈Rn:响应变量
-
λ>0:稀疏性调节参数
-
β∈Rd:系数向量
分解:
软阈值算子:
[proxh,η(z)]i=Sλ,η(zi)=⎩⎨⎧zi−ηλ0zi+ηλif zi>ηλif ∣zi∣≤ηλif zi<−ηλ
ISTA迭代公式:
βt+1=Sλη(βt+ηA⊤(y−Aβt))
推导说明:通过分析近端映射的一阶最优性条件,得到分段解析解,对应软阈值操作。
Mirror Descent
动机
考虑单纯形约束问题:
x∈△dminf(x)
其中 △d:={x∈Rd:∑i=1dxi=1,xi⩾0}。假设梯度满足 ∥∇f(x)∥∞⩽1,这意味着梯度的每个元素绝对值有界。
数学符号意义
-
∥⋅∥∞:无穷范数,表示向量中元素的最大绝对值,即 maxi∣xi∣。
-
∥⋅∥2:欧几里得范数,表示向量的标准长度,∥x∥2=∑ixi2。
-
L:Lipschitz常数,这里由梯度范数导出,∥∇f(x)∥2⩽d=L。
-
d:问题维度。
-
T:迭代次数。
-
f(xbest)−f(x∗):最优间隙,当前最佳解与最优解的函数值差。
-
ρ:强凸系数,用于描述镜像势能 Φ 的凸性强度。
-
η:步长,在Mirror Descent中设置为 η=L2RTρ。
-
R:定义域半径,R2=supx∈XDΦ(x,x1),其中 x1 是初始点。
预备知识
Mirror Descent 迭代过程
Mirror Descent 的迭代分为两步:对偶更新和投影。这个过程确保在每次迭代中,点都保持在可行域 X 内。
-
对偶更新步骤:
yt+1=(∇Φ)−1(∇Φ(xt)−ηtgt)
其中:
- xt 是当前迭代点(原始空间)。
- ∇Φ 是 Mirror Potential 的梯度,用于映射到对偶空间。
- ηt 是步长(学习率)。
- gt∈∂f(xt) 是目标函数 f 在 xt 处的次梯度(如果 f 可微,则为梯度)。这一步在对偶空间中执行梯度下降。
-
投影步骤:
xt+1=x∈XargminDΦ(x,yt+1)
其中 DΦ 是 Bregman Divergence 关联到 Φ。这一步将中间点 yt+1 投影回可行域 X,最小化 Bregman Divergence。
几何解释
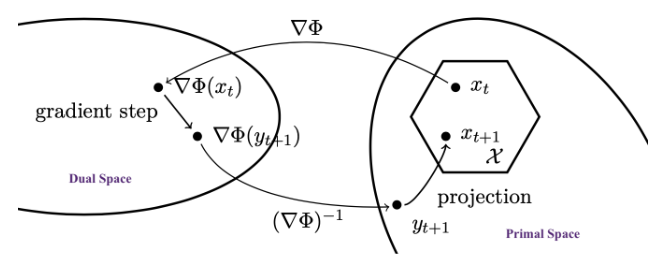
Mirror Descent 的几何意义可以从对偶空间和原始空间的角度理解:
- 对偶空间:梯度步骤 ∇Φ(xt)−ηtgt 在对偶空间中执行,这是一个线性更新。
- 原始空间:通过逆映射 (∇Φ)−1 将对偶点映射回原始空间,然后通过 Bregman 投影确保可行性。
- 示意图(如来自 Bubeck 2015)展示了这一过程:从对偶空间到原始空间的“镜像”映射,包括梯度步骤和投影,使算法在复杂几何下高效。
关键要素
Mirror Potential(镜像势函数)
Mirror Potential 是 Mirror Descent 的核心函数,记作 Φ。它定义了从原始空间到对偶空间的映射。
Bregman Divergence(Bregman 散度)
Bregman Divergence 是一种非对称距离度量,用于替代欧几里得距离,基于一个凸函数(通常为 Φ 或相关函数 f)。它定义了点之间的“差异”,并在投影步骤中用于确保可行性。
-
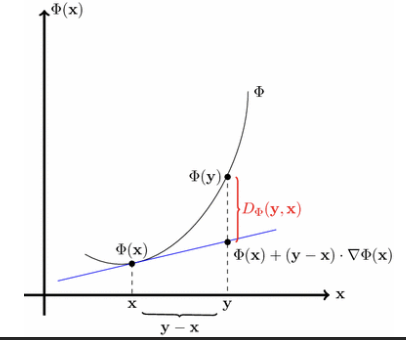
定义:对于函数 f,Bregman Divergence 定义为:
Df(x,y)=f(x)−f(y)−∇f(y)⊤(x−y)
这衡量了 x 和 y 之间的凸性差异。
-
性质:非负性(Df(x,y)≥0,且当 x=y 时等号成立)、凸性在 x 上。
投影算子
投影是 Mirror Descent 的关键部分,确保算法在约束集 X 上可行。
-
投影定义:投影操作记为 ΠXΦ,使用 Bregman Divergence 关联到 Φ:
ΠXΦ(y)=argx∈XminDΦ(x,y)
-
存在性与唯一性:由于 Φ 的严格凸性和连续可微性,投影 ΠXΦ 存在且唯一。这意味着对于任何点,都能找到唯一的投影点,避免算法的不确定性。
镜像下降法的收敛性
镜像下降法更新规则
镜像下降法(Mirror Descent)是一种优化算法,适用于非欧几里得空间中的凸优化问题。其更新规则如下:
核心思想:在镜像空间(由 Φ 定义)中执行梯度下降,然后通过镜像映射投影回原始空间。∇Φ 是映射的梯度,它将点从原始空间映射到对偶空间。
定理4: 收敛性保证
假设:
f(T1t=1∑Txt)−f(x∗)≤ρT2RL
其中 R 是初始点与最优解 x∗ 之间的“距离”上界,T 是迭代次数。
符号意义:
- ρ:强凸性参数,衡量 Φ 的凸性强度。
- L:Lipschitz 常数,表示函数 f 的变化率上界。
- R:通常定义为 R2=maxx∈XDΦ(x,x1),反映问题规模。
- η:步长,控制更新幅度,依赖于问题参数以确保收敛。
标准设置示例
Ball Setup(球设置)
-
镜像势能:Φ(x)=21∥x∥22
-
Bregman 散度:DΦ(x,y)=21∥x−y∥22
-
此时,Mirror Descent 等价于投影次梯度下降(Projected Subgradient Descent),因为投影在欧几里得空间中进行。
Simplex Setup(单纯形设置)
-
镜像势能:Φ(x)=∑i=1dxilogxi(负熵函数),定义在单纯形 △d={x∈Rd:xi≥0,∑ixi=1} 上。
-
梯度更新:∇Φ(yt+1)=∇Φ(xt)−η∇f(xt) 可写为分量形式:
yt+1,i=xt,iexp(−η[∇f(xt)]i)
-
Bregman 散度:DΦ(x,y)=∑i=1dxilogyixi(Kullback-Leibler 散度)。
-
投影:在单纯形上的投影等价于重归一化 y→y/∥y∥1。
-
例子:当 X=△d,初始点 x1=(1/d,…,1/d),则 R2=logd,这适用于高维概率优化。
例子说明:Simplex setup 常用于机器学习中的概率模型优化,如在线学习或约束在概率单纯形上的问题。KL 散度的使用使得算法更适应概率分布的几何。
证明细节:
-
基础不等式:利用Bregman散度的性质,有:
f(xt)−f(x)≤η1(DΦ(x,xt)−DΦ(x,xt+1))+2ρη∥gt∥∗2
- 来源:附件2 P47,通过一阶最优性条件和强凸性导出。
-
求和与 Telescoping:对 t=1 到 T 求和,DΦ 项形成 telescoping 和:
t=1∑T[DΦ(x,xt)−DΦ(x,xt+1)]=DΦ(x,x1)−DΦ(x,xT+1)≤R2
- 因为 x1=argminx∈XΦ(x),所以 DΦ(x,x1)≤R2。
-
界住梯度项:由于 f 是 L-Lipschitz,∥gt∥∗≤L,因此:
t=1∑T2ρη∥gt∥∗2≤2ρηTL2
-
结合结果:
t=1∑T(f(xt)−f(x))≤ηR2+2ρηTL2
- 选择 η=L2RTρ 最小化右端,得到收敛率。
-
Jensen不等式:最后应用 Jensen 不等式于平均点 T1∑t=1Txt。