SDSC6015 课程 5-镜像梯度下降与随机梯度下降

#sdsc6015

English / 中文

Mirror Descent

点击展开 Mirror Descent 复习内容

动机

考虑单纯形约束优化问题：

$$\min_{x \in \triangle_d} f(x)$$

其中单纯形 $\triangle_d := \{x \in \mathbb{R}^d : \sum_{i=1}^d x_i = 1, x_i \geq 0, \forall i\}$。假设梯度无穷范数有界：$\|\nabla f(x)\|_\infty = \max_{i=1,\ldots,d} |[\nabla f(x)]_i| \leq 1$。

• 符号说明：$x$ 是优化变量，$d$ 是维度，$\triangle_d$ 是概率单纯形。

• 几何意义：单纯形是概率分布空间，约束优化要求解在概率约束下最小化损失。

• 收敛率比较：

  • GD: $\mathcal{O}(\sqrt{d/T})$
  • Mirror Descent: $\mathcal{O}(\sqrt{\log d / T})$，在高维问题中更优。

初步知识

• 对偶范数：$\|g\|_* = \sup_{\|x\| \leq 1} g^\top x$。

• 函数性质：

  • $L$-Lipschitz: $\|g\|_* \leq L$ for $g \in \partial f(x)$。
  • $\beta$-光滑：梯度满足 Lipschitz 条件。
  • $\mu$-强凸：函数有下界二次项。

Mirror Descent 算法

迭代格式：

$$y_{t+1} = \nabla \Phi^*( \nabla \Phi(x_t) - \eta g_t ), \quad x_{t+1} = \Pi_X^\Phi(y_{t+1})$$

其中 $g_t \in \partial f(x_t)$，$\Phi$ 是镜像势能，$\Pi_X^\Phi$ 是基于 Bregman 散度的投影。

• 符号说明：$\Phi$ 严格凸、连续可微，$D_\Phi(x,y)$ 是 Bregman 散度。

• 几何意义：通过势能函数将问题变换到对偶空间，使更新方向更贴合几何结构。

收敛定理

定理 1（Mirror Descent 收敛性）：
设 $\Phi$ 是 $\rho$-强凸镜像映射，$R^2 = \sup_{x \in X} \Phi(x) - \Phi(x_1)$，$f$ 凸且 $L$-Lipschitz。取 $\eta = \frac{2R}{L} \sqrt{\frac{\rho}{T}}$，则：

$$\min_{t=1,\ldots,T} \mathbb{E}[f(x_t)] - f(x^*) \leq 2RL \sqrt{\frac{1}{\rho T}}$$

证明概要

1. 利用 Bregman 散度的强凸性 bound 误差。 2. 通过梯度 Lipschitz 性控制项。 3. 求和并优化步长。 详细见文档1第9页。

标准设置

• 球设置：$\Phi(x) = \frac{1}{2} \|x\|_2^2$，等价于投影梯度下降。

• 单纯形设置：$\Phi(x) = \sum_{i=1}^d x_i \log x_i$（负熵），Bregman 散度为 KL 散度，投影通过重归一化实现。

• 例子：在单纯形上优化概率分布时，Mirror Descent 自然处理约束，避免欧氏投影偏差。

---

随机梯度下降（Stochastic Gradient Descent, SGD）

---

问题形式

主问题定义为最小化一个函数 $f(\theta)$，其中 $\theta \in \mathbb{R}^d$ 是参数向量。具体形式如下：

$$\underset{\theta \in \mathbb{R}^d}{\text{minimize}} \, f(\theta)$$

这里，$f(\theta)$ 通常是一个期望损失函数，表示为：

$$f(\theta) = \int \ell(\theta, Z) \, dP(Z)$$

• $Z \in \mathbb{R}^p$ 是一个随机变量，代表数据点（如特征和标签）。

• $P(Z)$ 是未知的分布，这反映了在现实问题中数据分布往往不可知，只能通过样本估计。

• $\ell(\theta, Z)$ 是损失函数，参数化 by $\theta$，用于衡量模型在数据点 $Z$ 上的性能。

核心：通过最小化期望损失来学习参数 $\theta$，但由于 $P(Z)$ 未知，实际中我们使用经验风险最小化，即用样本均值近似积分。

给定一组带标签的训练数据 $(x_1, y_1), \ldots, (x_n, y_n) \in \mathbb{R}^d \times \mathcal{Y}$，目标是找到权重参数 $\theta$ 来对数据进行分类。这连接了优化问题与监督学习任务，如分类或回归。

简单来说，主问题就是通过优化参数 $\theta$ 来最小化模型在所有可能数据上的平均损失，但由于分布未知，我们依赖有限样本。

---

动机

当数据量巨大时（例如 $n \gg 1,000,000$），计算全梯度变得不切实际。具体分析如下：

• 定义 $f_i(\theta) = \ell(\theta, (x_i, y_i))$ 为第 $i$ 个观测值的成本函数，取自包含 $n$ 个观测的训练集。

• 全梯度 $\nabla f(\theta) = \sum_{i=1}^n \nabla f_i(\theta)$ 需要遍历所有数据点，计算成本随 $n$ 线性增长，当 $n$ 极大时，这会导致计算瓶颈。

• 因此，可以使用更便宜的方法：计算单个组件梯度 $\nabla f_i(\theta)$ 或小批量（batch）梯度。这引入了随机梯度下降（SGD）或其变种，通过随机采样数据点子集来近似梯度，从而大幅降低每次迭代的计算量。

---

SGD 算法描述

随机梯度下降的基本步骤如下：

• 初始化：设置初始点 $x_0 \in \mathbb{R}^d$。

• 迭代过程：对于每个时间步 $t = 0, 1, \ldots$：

  • 随机均匀采样一个索引 $i_t \in \{1, 2, \ldots, n\}$。
  • 更新参数： $x_{t+1} = x_t - \eta_t \nabla f_{i_t}(x_t)$，其中 $\eta_t$ 是学习率。

这里，$g_t := \nabla f_{i_t}(x_t)$ 被称为随机梯度，它仅使用单个函数组件 $f_{i_t}$ 的梯度，而不是全梯度 $\nabla f(x_t) = \frac{1}{n} \sum_{i=1}^n \nabla f_i(x_t)$。

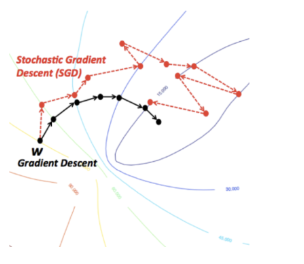
优点：计算效率

• 每次迭代只计算一个函数组件的梯度，因此迭代成本比全梯度下降（Full Gradient Descent）低 $n$ 倍。
• 这使得SGD在处理大数据集时更具可扩展性。

收敛性考虑

尽管SGD计算高效，但使用单个组件的梯度不一定保证收敛。文档中给出了一个例子来说明这个问题：

示例：考虑优化问题 $\min_x f(x) = f_1(x) + f_2(x)$，其中 $f_1(x) = x^2$ 和 $f_2(x) = -x^2$。如果从 $x_k > 0$ 开始，且随机采样到 $i_k = 2$，则梯度更新 $x_{k+1} = x_k - \eta_t \nabla f_2(x_k)$ 可能导致函数值增加（因为 $\nabla f_2(x) = -2x$，更新方向可能朝错误方向）。

然而，SGD在期望上可以产生下降，这引出了无偏性的概念。

无偏性（Unbiasedness）

随机梯度 $g_t$ 是真实梯度 $\nabla f(x_t)$ 的无偏估计，即：

$$\mathbb{E}[g_t|x_t = x] = \nabla f(x_t)$$

其中期望是对随机索引 $i_t$ 取的。

意义：无偏性确保在平均意义下，SGD的更新方向是正确的。尽管单个步骤可能随机偏离，但长期来看，算法会朝着最优解收敛。这允许我们使用期望不等式来分析收敛性，而不是依赖凸性等强假设。

---

条件期望

条件期望详解：

定义

条件期望是概率论和统计学中的核心概念，用于在已知部分信息（如另一个随机变量的值）下，对随机变量进行近似估计。

• 定义：设 X 和 Y 为随机变量。给定 Y 时 X 的条件期望，记为 $E[X|Y]$，是仅利用 Y 的信息对 X 的最佳近似。

  • 这与无条件期望 $E[X]$ 不同：$E[X]$ 给出 X 的整体平均值，而 $E[X|Y]$ 给出在已知 Y 值时 X 的平均值。
  • 直观上，条件期望“过滤”了 Y 的影响，提供了更精确的局部估计。

说明：条件期望在机器学习中常用于处理部分观测数据，例如在随机梯度下降中优化模型参数。

性质

• 线性性：条件期望是线性的，即对于随机变量 X 和 Y，以及常数 a 和 b，有：

  $$E[aX + bY | Z] = aE[X|Z] + bE[Y|Z]$$

  文档中暗示了类似性质，例如对于 Z = X + Y 或 Z = XY，条件期望可能满足加法或乘法规则，但具体公式未给出。

• Partition Theorem（分割定理）：针对离散随机变量 Y，该定理提供了计算期望的简化方法。

  • 定理表述：如果 Y 是离散随机变量，则无条件期望可以通过条件期望的期望来计算，即：

    $$E[X] = E[E[X|Y]]$$

    这表示先计算给定 Y 时 X 的条件期望，再对 Y 取期望。
  • 文档脚注指出，正式定义和性质可参考相关教材，这一定理是全期望定律（Law of Total Expectation）的特例。

示例：假设 Y 是离散的（如分类变量），则 $E[X]$ 可以通过对 Y 的每个可能值计算 $E[X|Y=y]$ 并加权平均得到。

期望的凸性

• 对于任意固定的 x，条件期望的线性性允许简化计算：

$$E[f(X)|Y] = \text{基于 Y 的线性组合}$$

其中 f 是凸函数。

• 文档提到事件 $\{x_t = x\}$ 仅对有限集 X 中的 x 发生（即 $x_t$ 由之前迭代的索引选择决定）。这暗示了在迭代算法（如随机梯度下降）中，参数更新仅限于有限选项。

• 应用 Partition Theorem：通过将期望分解为条件期望，可以简化凸性分析。例如：

$$E[L(x_t)] = E[E[L(x_t)|Y]]$$

其中 L 是损失函数，这有助于证明收敛性。

说明：在随机优化中，这种凸性分析确保算法即使在噪声数据下也能稳定收敛。

总结

文档重点介绍了条件期望的定义、性质（如线性性和 Partition Theorem）及其在凸性分析中的应用。这些概念是随机优化和机器学习的基础，有助于处理不确定性和部分信息。条件期望作为“最佳近似”工具，在模型训练和收敛证明中发挥关键作用。

注意：文档中提及的图片标签（如 ``）由于具体内容未提供，且为避免虚构，未在总结中嵌入。总结严格基于文本内容。

---

收敛定理

定理 2（凸函数上的 SGD）：
设 $f$ 凸可微，$x^*$ 是全局最优，$\|x_0 - x^*\| \leq R$，且 $\mathbb{E}[\|g_t\|^2] \leq B^2$。取常步长 $\eta = \frac{R}{B \sqrt{T}}$，则：

$$\frac{1}{T} \sum_{t=0}^{T-1}\mathbb{E} \left[ f(x_t) \right] - f(x^*) \leq \frac{RB}{\sqrt{T}}$$

证明详情（基于文档2 P23 补充）

证明概要：

1. 基础不等式：从迭代规则出发：

   $$\|x_{t+1} - x^*\|^2 = \|x_t - x^*\|^2 - 2\eta g_t^\top (x_t - x^*) + \eta^2 \|g_t\|^2$$

2. 取期望：利用无偏性 $\mathbb{E}[g_t | x_t] = \nabla f(x_t)$ 和凸性期望：

   $$\mathbb{E}[g_t^\top (x_t - x^*)] = \mathbb{E}[\nabla f(x_t)^\top (x_t - x^*)] \geq \mathbb{E}[f(x_t) - f(x^*)]$$

3. 求和优化：对 $t=0$ 到 $T-1$ 求和，并代入步长 $\eta = \frac{R}{B \sqrt{T}}$：

   $$\sum_{t=0}^{T-1} \mathbb{E}[f(x_t) - f(x^*)] \leq \frac{R^2}{2\eta} + \frac{\eta B^2 T}{2} = RB \sqrt{T}$$

4. Jensen 不等式：应用 $\mathbb{E}[f(\bar{x}_T)] \leq \frac{1}{T} \sum_{t=0}^{T-1} \mathbb{E}[f(x_t)]$，得最终界。

几何意义：SGD 在期望下沿下降方向移动，但方差导致振荡；步长调节平衡收敛速度和稳定性。

• 符号说明：$R$ 是初始误差界，$B$ 是随机梯度范数界，$T$ 是迭代次数。

• 与 GD 比较：全梯度下降的梯度范数界 $B_{\text{GD}}^2$ 通常小于 SGD 的 $B_{\text{SGD}}^2$（因 Jensen 不等式），但 SGD 每轮成本低，整体效率更高。

定理 3（强凸函数上的 SGD）：
设 $f$ $\mu$-强凸，$x^*$ 唯一最优，取步长 $\eta_t = \frac{1}{\mu t}$，则：

$$\mathbb{E}[\|x_T - x^*\|^2] \leq \frac{B^2}{\mu^2 T}$$

证明详情（基于文档2 P26 补充）

证明步骤：

1. 强凸性不等式：

   $$f(x^*) \geq f(x_t) + \nabla f(x_t)^\top (x^* - x_t) + \frac{\mu}{2} \|x_t - x^*\|^2$$

2. 迭代分析：代入 SGD 更新规则，取期望：

   $$\mathbb{E}[\|x_{t+1} - x^*\|^2] \leq (1 - \mu \eta_t) \mathbb{E}[\|x_t - x^*\|^2] + \eta_t^2 B^2$$

3. 递推求解：设 $\eta_t = 1/(\mu t)$，利用递推式求和得收敛界。

几何意义：强凸性确保函数有唯一最小点，SGD 以线性率收敛，但方差项 $B^2$ 影响精度。

小批量 SGD（Mini-batch SGD）

使用批量更新：$\tilde{g}_t = \frac{1}{|S_t|} \sum_{i \in S_t} \nabla f_i(x_t)$，其中 $S_t \subset \{1, \ldots, n\}$ 是随机子集。

• 符号说明：$|S_t| = m$ 是批量大小，$m=1$ 等价于 SGD，$m=n$ 等价于 GD。

• 方差计算（文档2 P31 补充）：

  $$\mathbb{E}[\|\tilde{g}_t - \nabla f(x_t)\|^2] = \frac{1}{m} \mathbb{E}[\|\nabla f_1(x_t) - \nabla f(x_t)\|^2] \leq \frac{B^2}{m}$$

  当 $m \to \infty$，方差趋于零。

• 几何意义：批量平均减少方差，使梯度估计更稳定，但每轮计算成本增加。

随机次梯度下降和约束优化

对于非光滑问题，使用次梯度 $g_t \in \partial f_i(x_t)$，更新为 $x_{t+1} = x_t - \eta_t g_t$。约束问题加入投影步骤（Projected SGD），收敛率仍为 $\mathcal{O}(1/\varepsilon^2)$。

---

动量方法（Momentum Methods）

动机

GD 在长窄谷形函数上振荡严重。动量方法引入历史步长信息加速收敛。

• 几何意义：动量像惯性球体，在平坦方向加速，在陡峭方向阻尼，减少振荡。

重球法（Polyak Momentum）

更新规则：

$$x_{t+1} = x_t - \eta_t \nabla f(x_t) + \beta_t (x_t - x_{t-1})$$

或等价写为：

$$v_{t+1} = \beta_t v_t - \eta_t \nabla f(x_t), \quad x_{t+1} = x_t + v_{t+1}$$

其中 $\beta_t \in [0,1]$ 是动量系数。

• 符号说明：$v_t$ 是动量项，$\beta_t$ 控制历史权重。

• 几何意义：动量项保留之前方向，帮助穿越局部平坦区。

收敛性

定理 4（二次函数上的收敛）：
考虑强凸二次函数 $f(x) = \frac{1}{2} x^\top Q x - b^\top x$，其中 $Q$ 正定，条件数 $\kappa = L/\mu$。取 $\eta_t = \frac{4}{(\sqrt{L} + \sqrt{\mu})^2}$，$\beta_t = \left( \frac{\sqrt{\kappa} - 1}{\sqrt{\kappa} + 1} \right)^2$，则重球法以线性率收敛。

证明概要

证明思路：

• 通过特征值分析，动量项改进了 GD 的收敛常数。

• 详细证明见文档1第39页及参考文献（如 Wright & Recht, 2022）。

几何意义：对于二次函数，动量调整步长以匹配 Hessian 矩阵的特征值分布，加速收敛。

• 反例（文档1第41-44页）：对于分段二次函数 $f(x)$，尽管是 1-强凸和 25-光滑，重球法可能循环不收敛（如取 $\eta_t = 1/9$, $\beta_t = 4/9$, $x_0 = 3.3$ 时迭代至三点循环）。

  • 几何意义：非光滑点导致动量方向错误，引发振荡。
  • 示意图：

Nesterov 加速梯度下降

与重球法类似，但使用预测点计算梯度，理论保证更鲁棒。更新规则差异：

• 重球法：直接结合当前梯度和动量。

• Nesterov 法：先沿动量方向移动，再计算梯度修正。

• 几何意义：Nesterov 法通过“前瞻”步骤减少振荡，更适合一般凸函数。

---