Mirror Descent

点击展开 Mirror Descent 复习内容

动机

考虑单纯形约束优化问题：

min⁡x∈△df(x)\min_{x \in \triangle_d} f(x)

其中单纯形 △d:={x∈Rd:∑i=1dxi=1,xi≥0,∀i}\triangle_d := \{x \in \mathbb{R}^d : \sum_{i=1}^d x_i = 1, x_i \geq 0, \forall i\}。假设梯度无穷范数有界：∥∇f(x)∥∞=max⁡i=1,…,d∣[∇f(x)]i∣≤1\|\nabla f(x)\|_\infty = \max_{i=1,\ldots,d} |[\nabla f(x)]_i| \leq 1。

  • 符号说明：xx 是优化变量，dd 是维度，△d\triangle_d 是概率单纯形。

  • 几何意义：单纯形是概率分布空间，约束优化要求解在概率约束下最小化损失。

  • 收敛率比较：

    • GD: O(d/T)\mathcal{O}(\sqrt{d/T})
    • Mirror Descent: O(log⁡d/T)\mathcal{O}(\sqrt{\log d / T})，在高维问题中更优。

初步知识

  • 对偶范数：∥g∥∗=sup⁡∥x∥≤1g⊤x\|g\|_* = \sup_{\|x\| \leq 1} g^\top x。

  • 函数性质：

    • LL-Lipschitz: ∥g∥∗≤L\|g\|_* \leq L for g∈∂f(x)g \in \partial f(x)。
    • β\beta-光滑：梯度满足 Lipschitz 条件。
    • μ\mu-强凸：函数有下界二次项。

Mirror Descent 算法

迭代格式：

yt+1=∇Φ∗(∇Φ(xt)−ηgt),xt+1=ΠXΦ(yt+1)y_{t+1} = \nabla \Phi^*( \nabla \Phi(x_t) - \eta g_t ), \quad x_{t+1} = \Pi_X^\Phi(y_{t+1})

其中 gt∈∂f(xt)g_t \in \partial f(x_t)，Φ\Phi 是镜像势能，ΠXΦ\Pi_X^\Phi 是基于 Bregman 散度的投影。

  • 符号说明：Φ\Phi 严格凸、连续可微，DΦ(x,y)D_\Phi(x,y) 是 Bregman 散度。

  • 几何意义：通过势能函数将问题变换到对偶空间，使更新方向更贴合几何结构。

收敛定理

定理 1（Mirror Descent 收敛性）：
设 Φ\Phi 是 ρ\rho-强凸镜像映射，R2=sup⁡x∈XΦ(x)−Φ(x1)R^2 = \sup_{x \in X} \Phi(x) - \Phi(x_1)，ff 凸且 LL-Lipschitz。取 η=2RLρT\eta = \frac{2R}{L} \sqrt{\frac{\rho}{T}}，则：

min⁡t=1,…,TE[f(xt)]−f(x∗)≤2RL1ρT\min_{t=1,\ldots,T} \mathbb{E}[f(x_t)] - f(x^*) \leq 2RL \sqrt{\frac{1}{\rho T}}

证明概要 1. 利用 Bregman 散度的强凸性 bound 误差。 2. 通过梯度 Lipschitz 性控制项。 3. 求和并优化步长。 详细见文档1第9页。

标准设置

  • 球设置：Φ(x)=12∥x∥22\Phi(x) = \frac{1}{2} \|x\|_2^2，等价于投影梯度下降。

  • 单纯形设置：Φ(x)=∑i=1dxilog⁡xi\Phi(x) = \sum_{i=1}^d x_i \log x_i（负熵），Bregman 散度为 KL 散度，投影通过重归一化实现。

  • 例子：在单纯形上优化概率分布时，Mirror Descent 自然处理约束，避免欧氏投影偏差。

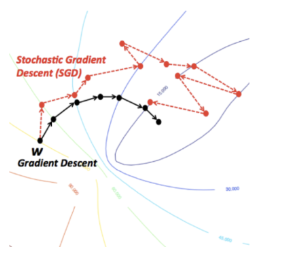
随机梯度下降（Stochastic Gradient Descent, SGD）

问题形式

主问题定义为最小化一个函数 f(θ)f(\theta)，其中 θ∈Rd\theta \in \mathbb{R}^d 是参数向量。具体形式如下：

minimizeθ∈Rd f(θ)\underset{\theta \in \mathbb{R}^d}{\text{minimize}} \, f(\theta)

这里，f(θ)f(\theta) 通常是一个期望损失函数，表示为：

f(θ)=∫ℓ(θ,Z) dP(Z)f(\theta) = \int \ell(\theta, Z) \, dP(Z)

  • Z∈RpZ \in \mathbb{R}^p 是一个随机变量，代表数据点（如特征和标签）。

  • P(Z)P(Z) 是未知的分布，这反映了在现实问题中数据分布往往不可知，只能通过样本估计。

  • ℓ(θ,Z)\ell(\theta, Z) 是损失函数，参数化 by θ\theta，用于衡量模型在数据点 ZZ 上的性能。

核心：通过最小化期望损失来学习参数 θ\theta，但由于 P(Z)P(Z) 未知，实际中我们使用经验风险最小化，即用样本均值近似积分。

给定一组带标签的训练数据 (x1,y1),…,(xn,yn)∈Rd×Y(x_1, y_1), \ldots, (x_n, y_n) \in \mathbb{R}^d \times \mathcal{Y}，目标是找到权重参数 θ\theta 来对数据进行分类。这连接了优化问题与监督学习任务，如分类或回归。

简单来说，主问题就是通过优化参数 θ\theta 来最小化模型在所有可能数据上的平均损失，但由于分布未知，我们依赖有限样本。

动机

当数据量巨大时（例如 n≫1,000,000n \gg 1,000,000），计算全梯度变得不切实际。具体分析如下：

  • 定义 fi(θ)=ℓ(θ,(xi,yi))f_i(\theta) = \ell(\theta, (x_i, y_i)) 为第 ii 个观测值的成本函数，取自包含 nn 个观测的训练集。

  • 全梯度 ∇f(θ)=∑i=1n∇fi(θ)\nabla f(\theta) = \sum_{i=1}^n \nabla f_i(\theta) 需要遍历所有数据点，计算成本随 nn 线性增长，当 nn 极大时，这会导致计算瓶颈。

  • 因此，可以使用更便宜的方法：计算单个组件梯度 ∇fi(θ)\nabla f_i(\theta) 或小批量（batch）梯度。这引入了随机梯度下降（SGD）或其变种，通过随机采样数据点子集来近似梯度，从而大幅降低每次迭代的计算量。

SGD 算法描述

随机梯度下降的基本步骤如下：

  • 初始化：设置初始点 x0∈Rdx_0 \in \mathbb{R}^d。

  • 迭代过程：对于每个时间步 t=0,1,…t = 0, 1, \ldots：

    • 随机均匀采样一个索引 it∈{1,2,…,n}i_t \in \{1, 2, \ldots, n\}。
    • 更新参数： xt+1=xt−ηt∇fit(xt)x_{t+1} = x_t - \eta_t \nabla f_{i_t}(x_t)，其中 ηt\eta_t 是学习率。

这里，gt:=∇fit(xt)g_t := \nabla f_{i_t}(x_t) 被称为随机梯度，它仅使用单个函数组件 fitf_{i_t} 的梯度，而不是全梯度 ∇f(xt)=1n∑i=1n∇fi(xt)\nabla f(x_t) = \frac{1}{n} \sum_{i=1}^n \nabla f_i(x_t)。

截屏2025-10-15 15.45.16.png

优点：计算效率

  • 每次迭代只计算一个函数组件的梯度，因此迭代成本比全梯度下降（Full Gradient Descent）低 nn 倍。
  • 这使得SGD在处理大数据集时更具可扩展性。

收敛性考虑

尽管SGD计算高效，但使用单个组件的梯度不一定保证收敛。文档中给出了一个例子来说明这个问题：

示例：考虑优化问题 min⁡xf(x)=f1(x)+f2(x)\min_x f(x) = f_1(x) + f_2(x)，其中 f1(x)=x2f_1(x) = x^2 和 f2(x)=−x2f_2(x) = -x^2。如果从 xk>0x_k > 0 开始，且随机采样到 ik=2i_k = 2，则梯度更新 xk+1=xk−ηt∇f2(xk)x_{k+1} = x_k - \eta_t \nabla f_2(x_k) 可能导致函数值增加（因为 ∇f2(x)=−2x\nabla f_2(x) = -2x，更新方向可能朝错误方向）。

然而，SGD在期望上可以产生下降，这引出了无偏性的概念。

无偏性（Unbiasedness）

随机梯度 gtg_t 是真实梯度 ∇f(xt)\nabla f(x_t) 的无偏估计，即：

E[gt∣xt=x]=∇f(xt)\mathbb{E}[g_t|x_t = x] = \nabla f(x_t)

其中期望是对随机索引 iti_t 取的。

意义：无偏性确保在平均意义下，SGD的更新方向是正确的。尽管单个步骤可能随机偏离，但长期来看，算法会朝着最优解收敛。这允许我们使用期望不等式来分析收敛性，而不是依赖凸性等强假设。

条件期望

条件期望详解：

定义

条件期望是概率论和统计学中的核心概念，用于在已知部分信息（如另一个随机变量的值）下，对随机变量进行近似估计。

  • 定义：设 X 和 Y 为随机变量。给定 Y 时 X 的条件期望，记为 E[X∣Y]E[X|Y]，是仅利用 Y 的信息对 X 的最佳近似。

    • 这与无条件期望 E[X]E[X] 不同：E[X]E[X] 给出 X 的整体平均值，而 E[X∣Y]E[X|Y] 给出在已知 Y 值时 X 的平均值。
    • 直观上，条件期望“过滤”了 Y 的影响，提供了更精确的局部估计。

说明：条件期望在机器学习中常用于处理部分观测数据，例如在随机梯度下降中优化模型参数。

性质

  • 线性性：条件期望是线性的，即对于随机变量 X 和 Y，以及常数 a 和 b，有：

    E[aX+bY∣Z]=aE[X∣Z]+bE[Y∣Z]E[aX + bY | Z] = aE[X|Z] + bE[Y|Z]

    文档中暗示了类似性质，例如对于 Z = X + Y 或 Z = XY，条件期望可能满足加法或乘法规则，但具体公式未给出。

  • Partition Theorem（分割定理）：针对离散随机变量 Y，该定理提供了计算期望的简化方法。

    • 定理表述：如果 Y 是离散随机变量，则无条件期望可以通过条件期望的期望来计算，即：

      E[X]=E[E[X∣Y]]E[X] = E[E[X|Y]]

      这表示先计算给定 Y 时 X 的条件期望，再对 Y 取期望。
    • 文档脚注指出，正式定义和性质可参考相关教材，这一定理是全期望定律（Law of Total Expectation）的特例。

示例：假设 Y 是离散的（如分类变量），则 E[X]E[X] 可以通过对 Y 的每个可能值计算 E[X∣Y=y]E[X|Y=y] 并加权平均得到。

期望的凸性

  • 对于任意固定的 x，条件期望的线性性允许简化计算：

E[f(X)∣Y]=基于 Y 的线性组合E[f(X)|Y] = \text{基于 Y 的线性组合}

其中 f 是凸函数。

  • 文档提到事件 {xt=x}\{x_t = x\} 仅对有限集 X 中的 x 发生（即 xtx_t 由之前迭代的索引选择决定）。这暗示了在迭代算法（如随机梯度下降）中，参数更新仅限于有限选项。

  • 应用 Partition Theorem：通过将期望分解为条件期望，可以简化凸性分析。例如：

E[L(xt)]=E[E[L(xt)∣Y]]E[L(x_t)] = E[E[L(x_t)|Y]]

其中 L 是损失函数，这有助于证明收敛性。

说明：在随机优化中，这种凸性分析确保算法即使在噪声数据下也能稳定收敛。

总结

文档重点介绍了条件期望的定义、性质（如线性性和 Partition Theorem）及其在凸性分析中的应用。这些概念是随机优化和机器学习的基础，有助于处理不确定性和部分信息。条件期望作为“最佳近似”工具，在模型训练和收敛证明中发挥关键作用。

注意：文档中提及的图片标签（如 ``）由于具体内容未提供，且为避免虚构，未在总结中嵌入。总结严格基于文本内容。

收敛定理

定理 2（凸函数上的 SGD）：
设 ff 凸可微，x∗x^* 是全局最优，∥x0−x∗∥≤R\|x_0 - x^*\| \leq R，且 E[∥gt∥2]≤B2\mathbb{E}[\|g_t\|^2] \leq B^2。取常步长 η=RBT\eta = \frac{R}{B \sqrt{T}}，则：

1T∑t=0T−1E[f(xt)]−f(x∗)≤RBT\frac{1}{T} \sum_{t=0}^{T-1}\mathbb{E} \left[ f(x_t) \right] - f(x^*) \leq \frac{RB}{\sqrt{T}}

证明详情（基于文档2 P23 补充）

证明概要：

  1. 基础不等式：从迭代规则出发：

    ∥xt+1−x∗∥2=∥xt−x∗∥2−2ηgt⊤(xt−x∗)+η2∥gt∥2\|x_{t+1} - x^*\|^2 = \|x_t - x^*\|^2 - 2\eta g_t^\top (x_t - x^*) + \eta^2 \|g_t\|^2

  2. 取期望：利用无偏性 E[gt∣xt]=∇f(xt)\mathbb{E}[g_t | x_t] = \nabla f(x_t) 和凸性期望：

    E[gt⊤(xt−x∗)]=E[∇f(xt)⊤(xt−x∗)]≥E[f(xt)−f(x∗)]\mathbb{E}[g_t^\top (x_t - x^*)] = \mathbb{E}[\nabla f(x_t)^\top (x_t - x^*)] \geq \mathbb{E}[f(x_t) - f(x^*)]

  3. 求和优化：对 t=0t=0 到 T−1T-1 求和，并代入步长 η=RBT\eta = \frac{R}{B \sqrt{T}}：

    ∑t=0T−1E[f(xt)−f(x∗)]≤R22η+ηB2T2=RBT\sum_{t=0}^{T-1} \mathbb{E}[f(x_t) - f(x^*)] \leq \frac{R^2}{2\eta} + \frac{\eta B^2 T}{2} = RB \sqrt{T}

  4. Jensen 不等式：应用 E[f(xˉT)]≤1T∑t=0T−1E[f(xt)]\mathbb{E}[f(\bar{x}_T)] \leq \frac{1}{T} \sum_{t=0}^{T-1} \mathbb{E}[f(x_t)]，得最终界。

几何意义：SGD 在期望下沿下降方向移动，但方差导致振荡；步长调节平衡收敛速度和稳定性。

  • 符号说明：RR 是初始误差界，BB 是随机梯度范数界，TT 是迭代次数。

  • 与 GD 比较：全梯度下降的梯度范数界 BGD2B_{\text{GD}}^2 通常小于 SGD 的 BSGD2B_{\text{SGD}}^2（因 Jensen 不等式），但 SGD 每轮成本低，整体效率更高。

定理 3（强凸函数上的 SGD）：
设 ff μ\mu-强凸，x∗x^* 唯一最优，取步长 ηt=1μt\eta_t = \frac{1}{\mu t}，则：

E[∥xT−x∗∥2]≤B2μ2T\mathbb{E}[\|x_T - x^*\|^2] \leq \frac{B^2}{\mu^2 T}

证明详情（基于文档2 P26 补充）

证明步骤：

  1. 强凸性不等式：

    f(x∗)≥f(xt)+∇f(xt)⊤(x∗−xt)+μ2∥xt−x∗∥2f(x^*) \geq f(x_t) + \nabla f(x_t)^\top (x^* - x_t) + \frac{\mu}{2} \|x_t - x^*\|^2

  2. 迭代分析：代入 SGD 更新规则，取期望：

    E[∥xt+1−x∗∥2]≤(1−μηt)E[∥xt−x∗∥2]+ηt2B2\mathbb{E}[\|x_{t+1} - x^*\|^2] \leq (1 - \mu \eta_t) \mathbb{E}[\|x_t - x^*\|^2] + \eta_t^2 B^2

  3. 递推求解：设 ηt=1/(μt)\eta_t = 1/(\mu t)，利用递推式求和得收敛界。

几何意义：强凸性确保函数有唯一最小点，SGD 以线性率收敛，但方差项 B2B^2 影响精度。

小批量 SGD（Mini-batch SGD）

使用批量更新：g~t=1∣St∣∑i∈St∇fi(xt)\tilde{g}_t = \frac{1}{|S_t|} \sum_{i \in S_t} \nabla f_i(x_t)，其中 St⊂{1,…,n}S_t \subset \{1, \ldots, n\} 是随机子集。

  • 符号说明：∣St∣=m|S_t| = m 是批量大小，m=1m=1 等价于 SGD，m=nm=n 等价于 GD。

  • 方差计算（文档2 P31 补充）：

    E[∥g~t−∇f(xt)∥2]=1mE[∥∇f1(xt)−∇f(xt)∥2]≤B2m\mathbb{E}[\|\tilde{g}_t - \nabla f(x_t)\|^2] = \frac{1}{m} \mathbb{E}[\|\nabla f_1(x_t) - \nabla f(x_t)\|^2] \leq \frac{B^2}{m}

    当 m→∞m \to \infty，方差趋于零。

  • 几何意义：批量平均减少方差，使梯度估计更稳定，但每轮计算成本增加。

随机次梯度下降和约束优化

对于非光滑问题，使用次梯度 gt∈∂fi(xt)g_t \in \partial f_i(x_t)，更新为 xt+1=xt−ηtgtx_{t+1} = x_t - \eta_t g_t。约束问题加入投影步骤（Projected SGD），收敛率仍为 O(1/ε2)\mathcal{O}(1/\varepsilon^2)。

动量方法（Momentum Methods）

动机

GD 在长窄谷形函数上振荡严重。动量方法引入历史步长信息加速收敛。

  • 几何意义：动量像惯性球体，在平坦方向加速，在陡峭方向阻尼，减少振荡。

重球法（Polyak Momentum）

更新规则：

xt+1=xt−ηt∇f(xt)+βt(xt−xt−1)x_{t+1} = x_t - \eta_t \nabla f(x_t) + \beta_t (x_t - x_{t-1})

或等价写为：

vt+1=βtvt−ηt∇f(xt),xt+1=xt+vt+1v_{t+1} = \beta_t v_t - \eta_t \nabla f(x_t), \quad x_{t+1} = x_t + v_{t+1}

其中 βt∈[0,1]\beta_t \in [0,1] 是动量系数。

  • 符号说明：vtv_t 是动量项，βt\beta_t 控制历史权重。

  • 几何意义：动量项保留之前方向，帮助穿越局部平坦区。

收敛性

定理 4（二次函数上的收敛）：
考虑强凸二次函数 f(x)=12x⊤Qx−b⊤xf(x) = \frac{1}{2} x^\top Q x - b^\top x，其中 QQ 正定，条件数 κ=L/μ\kappa = L/\mu。取 ηt=4(L+μ)2\eta_t = \frac{4}{(\sqrt{L} + \sqrt{\mu})^2}，βt=(κ−1κ+1)2\beta_t = \left( \frac{\sqrt{\kappa} - 1}{\sqrt{\kappa} + 1} \right)^2，则重球法以线性率收敛。

证明概要

证明思路：

  • 通过特征值分析，动量项改进了 GD 的收敛常数。

  • 详细证明见文档1第39页及参考文献（如 Wright & Recht, 2022）。

几何意义：对于二次函数，动量调整步长以匹配 Hessian 矩阵的特征值分布，加速收敛。

  • 反例（文档1第41-44页）：对于分段二次函数 f(x)f(x)，尽管是 1-强凸和 25-光滑，重球法可能循环不收敛（如取 ηt=1/9\eta_t = 1/9, βt=4/9\beta_t = 4/9, x0=3.3x_0 = 3.3 时迭代至三点循环）。

    • 几何意义：非光滑点导致动量方向错误，引发振荡。
    • 示意图：

Nesterov 加速梯度下降

与重球法类似，但使用预测点计算梯度，理论保证更鲁棒。更新规则差异：

  • 重球法：直接结合当前梯度和动量。

  • Nesterov 法：先沿动量方向移动，再计算梯度修正。

  • 几何意义：Nesterov 法通过“前瞻”步骤减少振荡，更适合一般凸函数。